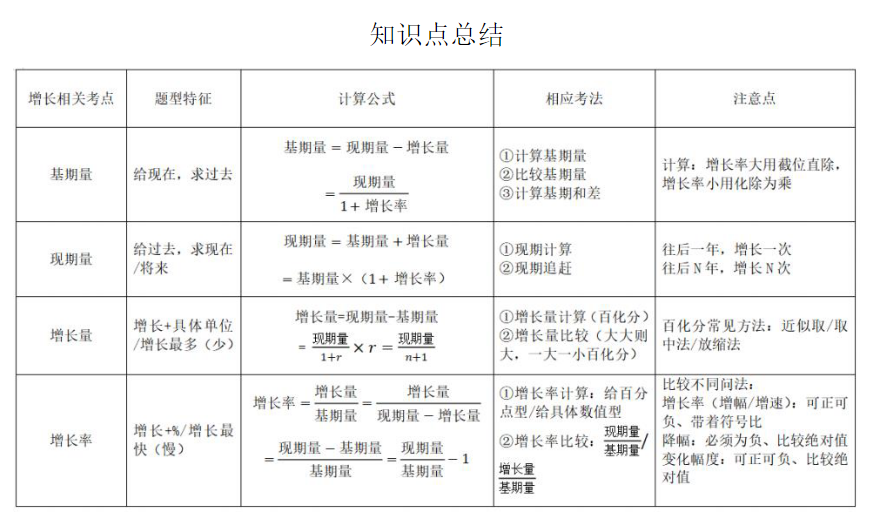
资料分析
第一节 速算技巧
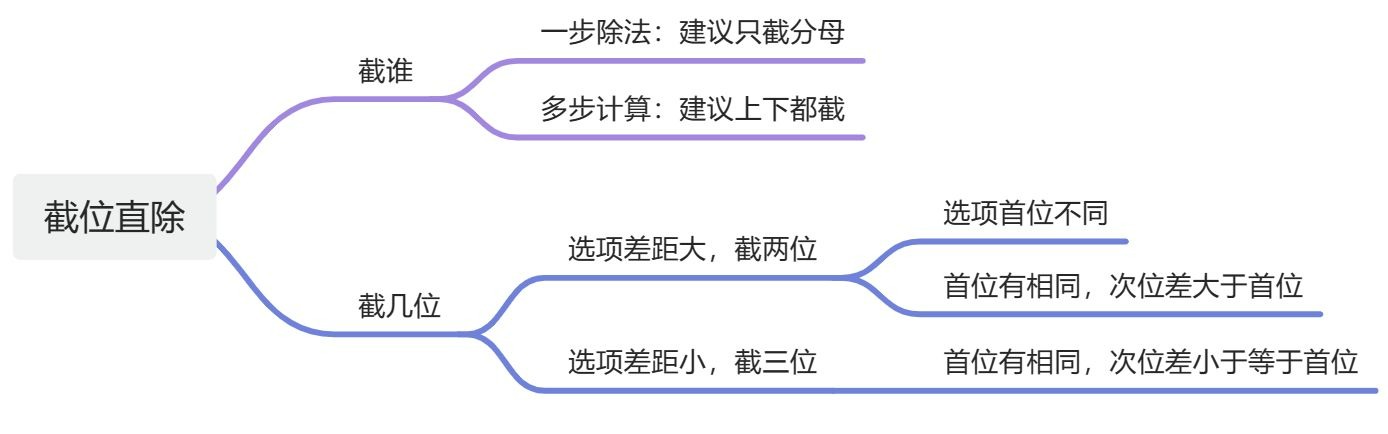
一、截位直除
【注意】什么是截位?1、截位:从左往右截,截几位保留几位(分为两类:截两位–>保留前两位,截三位–>保留前三位),下一位四舍五入(4 以及4以下的–>舍去,5 以及5以上的–>进位),截位时从第一个非0的数开始。
2、示例 1:12365。
(1)截两位:保留前两位 12,下一位是3(在4以下),舍去,截完两位为12。
(2)截三位:保留前三位 123,下一位是6(在5以上),进位,则截三位为 124。
3、截位时从第一个非0的数开始。只看有效数字就行,如 0.04567,前面的”0.0”不用看,只用对 4567 进行截位。
(1)截两位:保留前两位 45,第三位是 6,进位,截两位为 46。
(2)截三位:保留前三位 456,第四位是 7,进位,截三位为 457。
【注意】截谁:看算式形式。以截两位举例子。1、一步除法(通俗来讲就是一个除号):只截分母。
例:。
答:只有一个除号,属于一步除法,只截分母。影响除法计算难度的是分母,分母越短越好,以截两位为例,原式转化为。如果截分子,转化为,除的时候分子后面还需要补三个“0”,不会影响计算难度,故一步除法只截分母即可。
2、多步除法(多个除号):分子分母都截(截完约分)。
例:。
答:有两个除号,属于多步除法,只截分母计算难度还是很大,分子、分母都截位。以截两位举例,转化为,先约分,,,即原式=。
【注意】截几位——看选项(大则截两位,小则截三位):选项差距大,截两位计算;选项差距小,截三位计算。原理:截两位-->选项差距大时,胆子可以大一些,估算即可,故截两位;截三位-->选项差距小时,截两位虽然好算,但是不够精确,所以要截三位。1、选项差距大(截两位):
(1)首位(数字)均不相同:
示例 1:A.65、B.53、C.47、D.38。选项首位 6、5、4、3 各不相同,选项差距大。
(2)首位有相同,看次位差(第二位的差值)>首位。
示例 2:A.65、B.53、C.59、D.47。B、C项的首位均为5,首位有相同,直接看 B、C项的次位差,看次位差是否大于首位,次位差= 9 - 3 = 6 > 首位5,选项差距大。
2、选项差距小(截三位):首位有相同,次位差 ≤ 首位。
(1)示例 3:A.65、B.53、C.58、D.47。B、C项首位均为5,次位差= 8 - 3 = 5首位 5,选项差距小。
(2)示例 4:A.59、B.53、C.52、D.47。A、B、C项首位均为5,计算时找最接近的两个选项,如果找两个远的可能会判断为差距大,B、C项最接近,次位差= 3 - 2 = 1 < 首位5,选项差距小,截三位。
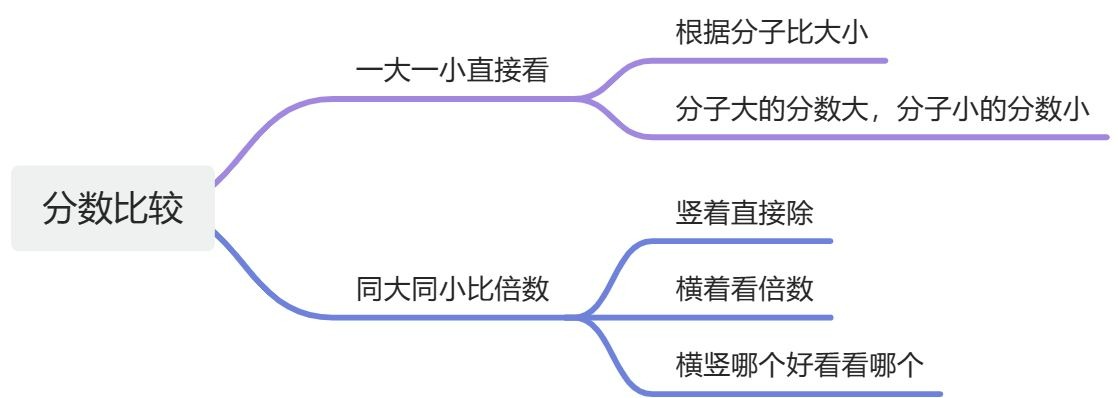
二、分数比较
【注意】一大一小直接瞪:1、两个分数比较,如果一个分数,它的分子大、分母小,则这个分数大。
例:和比较。
答:的分子大、分母小,则分数值大,故>。
2、举个例子:分钱。A 单位有 200 万、3 个人分,B 单位有 50 万、6 个人分。此时肯定更想去A单位,A单位是“钱多人少”,分到的钱更多,B单位是“人多钱少”,分到的钱少。钱数代表的是分子,人数代表的是分母,“钱多人少”分的钱越多,就是分子大分母小值越大。即一大一小可以理解为“钱多人少”。
【注意】同大同小:分子、分母同时大或同时小。1、竖着直接除:
(1)看商几,谁的商大谁就大。
(2)例:和比较。
答:分子分母同大同小,不能直接瞪,竖着直接除。首位商不到5,首位商7,则<。
2、横着看倍数:分子和分子之间看倍数,分母和分母之间看倍数。
(1)分子倍数大,只看分子,则分子大的分数大。
例:和比较。
答:分子:150→450为3倍,分母:22→44为2倍,分子倍数大,只看分子,分子大的分数大,则< 。
(2)分母倍数大,只看分母,则分母大的分数小。
例:和 比较。
答:分子之间:300是150的2倍,分母之间:66是22的3倍,分母倍数大,只看分母,分母大的分数小,则>。
(3)原理:本质就是通分。
第二节 基期与现期
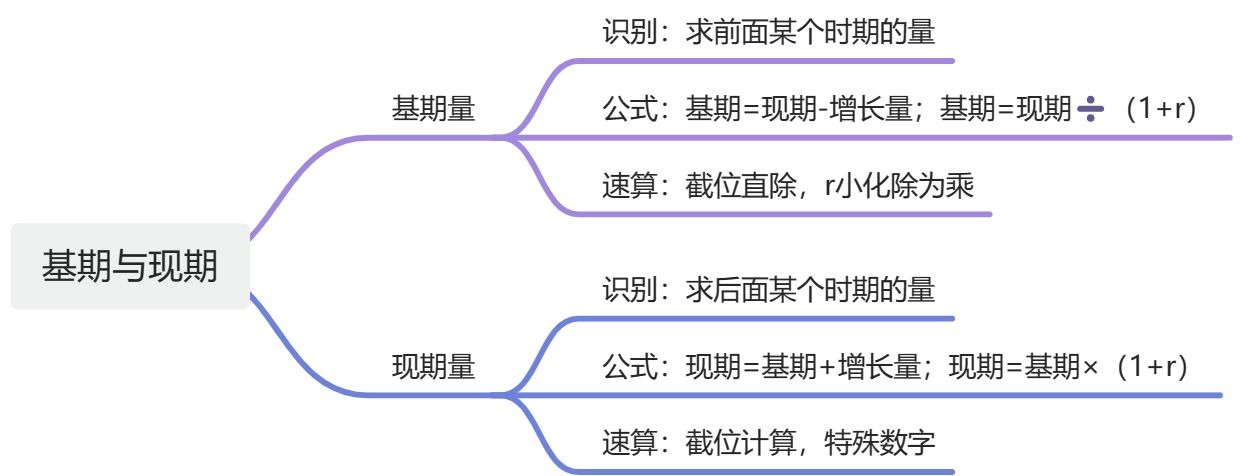
一、基期量
【注意】基期量(重点):1、题型识别:基期相当于过去,基期量相当于求过去的值。如材料给 2023年,求 2022年,给现在,求过去,求基期,重点是把时间看清楚。
2、计算公式:根据数据不同,公式也不一样。
(1)基期量= 现期量 - 增长量
例:2023 年为 120 公斤,比2022年增长了20公斤,求2022年。
答:基期量 = 现期量 - 增长量 → 2022年 = 120 - 20 = 100 公斤。
(2)基期量=(r 代表增长率,增长率的英文是 rate),绝大多数考的是这个公式,r代表增长率。
①例:2023 年体重为 120 公斤,比 2022 年增长了 20%,求 2022 年。
答:→2022年=。
②例:2023 年体重为 120 公斤,比 2022 年下降了 20%,求 2022 年。
答:→2022年=。
3、速算技巧:截位直除。
【注意】拓展一组基本术语--同比与环比:1、同比:与上年同期相比。
2、环比:与紧紧相邻的上一统计周期相比(月环比、季度环比)
3、例:
(1)2022年7月:同比是2021年7月(把年份往前推一年),环比是 2022年6月(年份不变,把月份往前推一个月)。
(2)2022年三季度:同比是2021年三季度(把年份往前推一年),环比是2022年二季度(年份不变,季度往前推一个季度)。
4、简单记:同比看年(同比往前推一年),环比看尾(环比看“尾巴”,尾巴给的是月份,往前推一个月;尾巴给的是季度,往前推一个季度)
【注意】化除为乘:1、应用:,|r| ≤ 5%。
2、方法:假设现期量是 A。
(1)增长率为负:。
(2)增长率为正:。
3、记忆方法:变号。比如,r = 2 % < 5%,化除为乘转化为。如,化除为乘转化为。
4、推导(考试不考,能听就听,不懂也没关系):的分子、分母同时乘以一个数(1+r),分数值大小不变,得到,此时分母为著名的平方差公式,,原式转化为。r = 5% → r² = 5% * 5% = 0.0025,r非常小,可以看成 0,此时 1 - r ≈ 1,则。
【注意】基期和差:1、公式:
2、方法:
(1)观察选项:通过正、负排除,基本可以排除两个选项。
(2)以坑治坑:排除现期坑,求的是基期差,排除现期差。
(3)治不了:估算 / 截位直除
二、现期量
【注意】现期量:讲的少是因为考情,基期量考查多,现期量考查少,但是从去年开始每次都考1道题,需要作为一个重点去学习。现期量比较好学,和基期量是反过来的。1、题型识别:给基期,求以后某时期的值。给过去求现在或将来,如给 2022年,求 2023 年。
2、计算公式:
(1)给基期量和增长量:
①现期量 = 基期量 + 增长量(基期量 = 现期量 - 增长量 → 现期量 = 基期量 + 增长量)。例:2022年为 100 公斤,2023 年比 2022年增长量 20公斤,则2023年=100+20=120。
②现期追赶问题:如例题中问的是过了一年增长 20 斤是多少斤,现期追赶问题问的是过4年之后是多少斤:过了不止一年→现期追赶,所求=100+20 * 4=180;过n年:所求=100+20 * n。
(2)现期量 = 基期量 * (1+r)。例 2022 年为 100 公斤,2023 年比 2022 年增长量 20%,则 2023 年=100 * (1+20%);用这个公式考查“过n年”的情况在联考中比较少。
3、速算技巧:截位/特殊数字。
(1)特殊数字是前半节课讲解的 A * 1.1→错位相加、A * 0.9→错位相减。
(2)乘法也可以截位,只是用的没那么多,有时候会用一些百化分的技巧,如1234 * (1+25%)=1234 * (1+1/4)
第三节 一般增长率
【注意】百分数与百分点:1、概念:
(1)百分数:表示两个量的比例关系,用除法计算。如男生是 30 人,全班人数为 100 人,男生占全班的比重为。
(2)百分点:表示百分数的变化,用加减法计算,两个百分数相减,单位是百分点,比如我的增长率为 10%,你的增长率为5%,此时我的增长率比你的增长率多 109-59=5 个百分点。
2、考查形式:给出一个百分数和百分点,求另一个百分数,用加减。
(1)例 1:2023 年收入同比增长 10%,增速比去年提高5个百分点。则 2022年的增长率为?
答:今年比去年提高,说明今年高、去年低。求去年,需要减去,所求=10%-5%=5%。
(2)例 2:2023 年收入同比增长 10%,增速比去年回落5个百分点。则 2022年的增长率为?
答:“回落”就是降低,说明今年低、去年高。求去年,需要加上59,所求=10%+5%=15%。
3、口诀:高减低加。出现“提高”用减法,出现“降低”用加法。
【注意】增长率与倍数:1、倍数:A是B的几倍,谁是谁的几倍。
(1)公式:是几倍=。
(2)例:已知 2022 年工资是 15 万元,2021 年是 10 万元。问 2022 年工资是 2021 年工资的几倍。
答:相当于 2022年是A,2021年是B,倍数=倍
2、增长率:A 比B增长了百分之几。
(1)公式:增长率=。
(2)例:已知 2022 年工资是 15 万元,2021 年是 10 万元,求增长率。
答:。
3、同样的例子,增长率是 0.5,倍数是 1.5,则 r+1=倍数。
4、两者关系:倍数 = 增长率 + 1。在间隔增长率部分可能会用到,或在综合分析的某个选项可能会考查,如增长率为30%,问今年是去年的几倍,倍数为1+30%=1.3 倍
【注意】成数与翻香1、成数:几成相当于十分之几,即百分之几十。看到成数可以自然的转化为百分数,比如三成=3/10=30%,四成=4/10=40%,三成多=30%≈40%。
2、翻番:
(1)翻1番:原来的2倍;翻2番:在翻1番的基础上再翻1番→2 倍 * 2倍,即原来的4倍;翻n番:原来的2^n倍(重点记忆)
(2)例:
①100翻3番,变为多少?
答:翻3番=2³=8倍,所求=100 * 8 = 800。
②100 到 1600,翻了几番?
答:1600/100=16倍=2”,则n=4,即翻了4番。
一、一般增长率
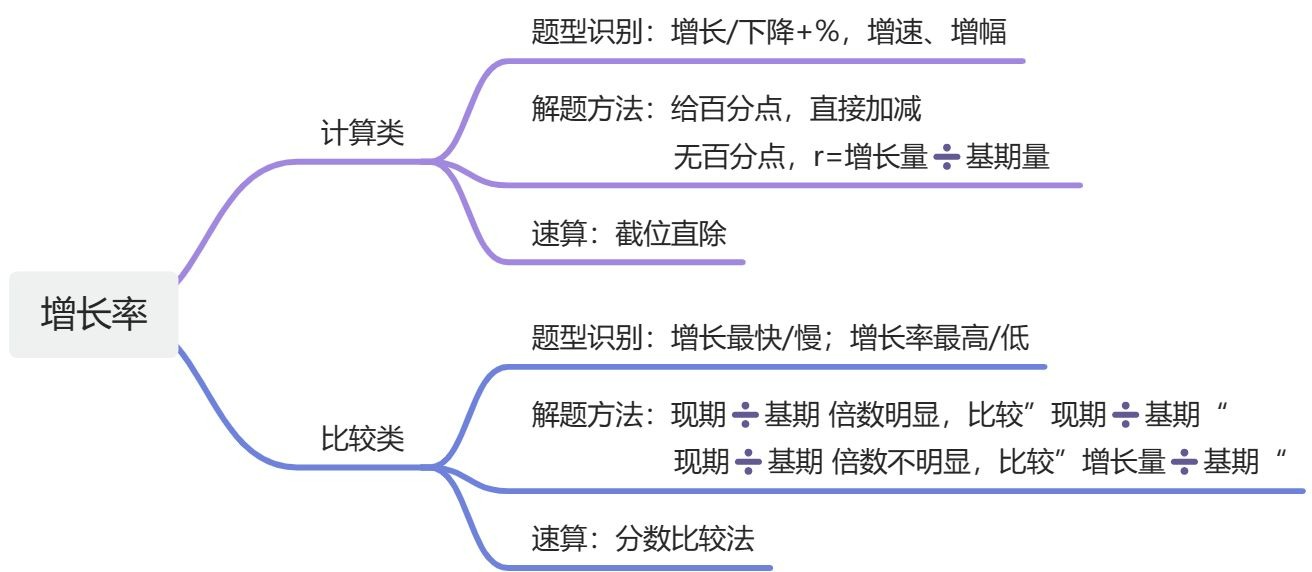
【注意】增长率计算:1、题型识别:增长率/增速/增幅(增长幅度),增长/下降+%。
2、题型:
(1)给百分点,加减法。口诀:高减低加。可能会结合其他的大题进行考查,不太可能单独作为一道题出。
例:今年增长率为 10%,比去年提高了3个百分点,求去年增长率?
答:高减低加,出现“提高”,需要减去,去年增长率=10%-3%=7%。
(2)给具体量,套公式。以下三种公式都是同一个公式,只是形式不同而已。
①,若刚开始学习,比较乱,觉得公式不好记忆,只需要记原始式公式即可,后两个公式都是根据这个公式变形而来。
②基期=现期 - 增长量,则
③增长量=现期 - 基期,则
3、速算技巧:截位直除。
二、比较类
【注意】增长率比较:1、题型识别:
(1)增长率最高/最低
(2)增长最快/最慢(考查最多,容易识别错误):关键在于“快、慢”,增长率又叫做增长速度,快、慢形容的是速度,因此出现“快、慢”是增长率比较。
2、计算公式:。注意不要用“r=现期量/基期量-1”进行计算,只用于结论推导,增长率的大小和“-1”没有关系,关键在于“现期量/基期量”,故“现期量/基期量越大,增长率就越大”。
3、比较方法:
(1)现期与基期倍数关系明显:用“现期量/基期量”比较。如一道题中问A、B、C、D项哪个选项的增长率最大,将每个选项的现期/基期除完之后,选项分别为A、1+、B、2+、C、3+、D、4+,明显D项倍数关系最大,D 项的增长率最大,能够一眼看出来谁大谁小,称为倍数关系明显。
(2)现期与基期倍数关系不明显:用“增长量/基期量”比较。如果现期基期除完之后,四个选项都是1倍,这叫倍数关系不明显,说明“现期量/基期量”不好用,只能用原始公式“增长量/基期量”进行比较。
(3)优先用“现期/基期”,不能用则用“增长量/基期’
4、做题要有灵魂,三步走
(1)第一步,确定基期、现期。
(2)第二步直接看“现期/基期”能否得到唯一答案。
(3)第三步,不能得出,再比较“增长量/基期”。
第四节 增长量
一、计算类
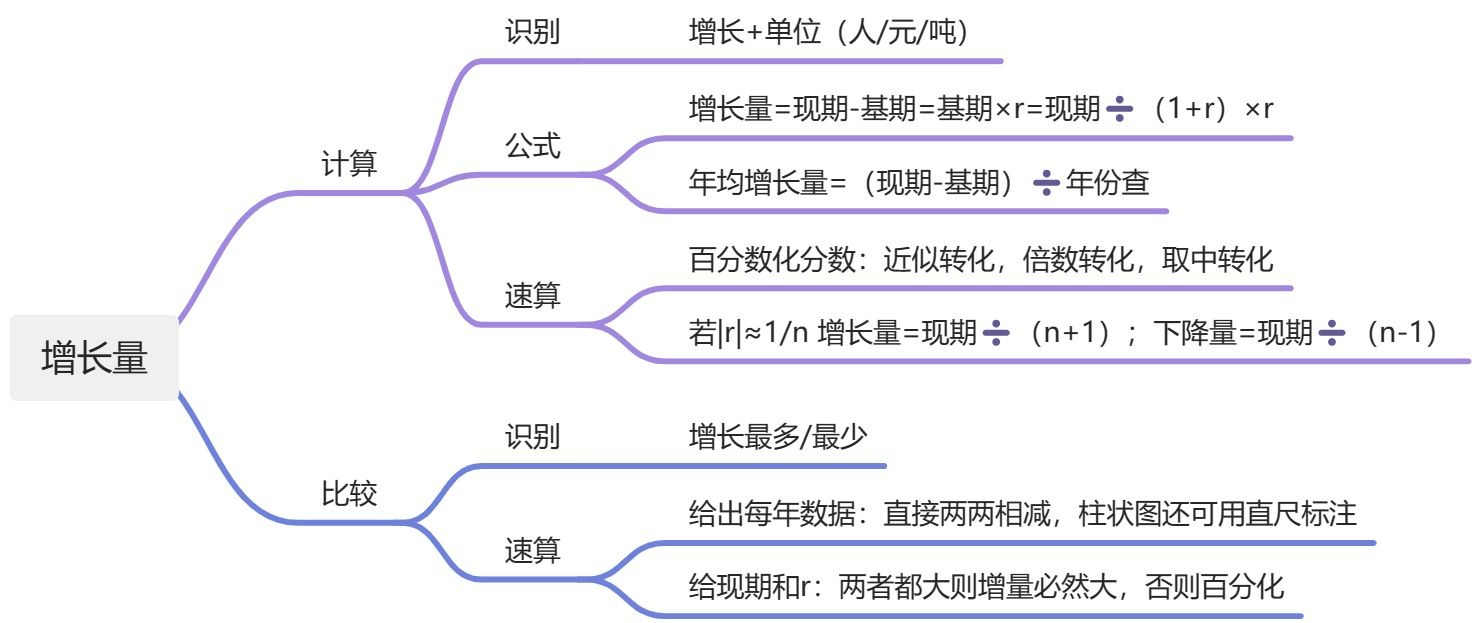
【注意】增长量计算:1、题型识别:增长+%是增长率;同样是增长率,增长+具体值是增长量,比如 2019 年比 2018 年增长了多少万人/亿元/吨。
2、计算公式:
(1)给现期和基期(太简单,考查较少):增长量=现期量-基期量。
(2)给现期和增长率:
①公式:增长量 = ,不用背,后面会讲解计算方法(百化分)。
②公式的由来:,增长量=基期 * r;,。
【注意】年均增长量:1、题型识别:年均、平均每年+增长+单位。
2、公式:,n 为现期和基期的年份差。
3、重点:基期的确定、n 的取值。
【注意】年均增长问题基期的确定:1、具体时间段(一般情况):直接给时间段,2011~2015 年。
(1)基期时间:开头的时间,为 2011年。
(2)现期时间:结尾的时间,为 2015 年。
(3)年份差=现期年份-基期年份=2015-2011=4。
2、五年规划(特殊情况):如“十二五”期间(2011~2015 年)。
(1)年份差:国家规定为5年。
(2)基期时间:按照常规算法,年份差为2015-2011=4,但为了保证年份差为 5,基期必须往前推一年,为 2010年。
(3)现期时间:2015 年。
(4)“十四五”(2021~2025 年);“十三五”(2016~2020年);“十二五(2011~2015 年),常考“十二五”和“十三五”(“十四五”还没过完,“十一五”太久远)。
【注意】已知现期量和r,求增长量:1、公式:增长量 =。
2、速算:百化分两步走。
(1)增长率百化分:百分数化成分数。|r|=1/n。r=25%可以化成 1/4,则n=4,n 就代表分数的分母,再比如r=20%可以化成 1/5,则n=5。
(2),。
3、例:2016 年总收入是 100 万元,同比增长 25%。求:2016 年与 2015 年相比总收入增长了多少万元?
答:已知现期量和增长率,求增长量,方法为百化分。
(1)增长率转化为 1/n。25%=1/4,则 n=4
(2)增长量=现期/(n+1)=100/(4+1)=100/5=20
4、公式推导:将r转化成 1/n,则。减少量公式的推导过程同理。
5、例:2016 年总收入是 100 万元,同比下降 25%。求:2016 年与 2015 年相比总收入下降了多少万元?
答:已知现期量和r,求减少量。百化分:|-25%|=1/4,则n=4。减少量=现期量/(n-1)=100/(4-1)=100/3=33.3。
【注意】百化分:1、两倍的关系:
(1);;
(2);;
(3);;
2、一组数,可以互相转化:
(1) 7和14是一组数,7 * 14≈100
(2) 9和11是一组数,9 * 11≈100
3、记忆:
4、等差数列“5.963”:
【注意】增长率百化分之放缩法(倍数法):利用与背过的百分数的倍数关系,实现百化分。1、因 r=1/n,所以r与n成反比关系,r越大,则n越小,反之相同
2、例:
(1)2.5%:25%=1/4,从25%到2.5%,增长率缩小 10 倍,n 要扩大 10 倍则2.5%=1/40。
(2)250%:25%=1/4,增长率从25%到250%扩大10倍,n要缩小 10 倍,则250%=1/0.4。
(3)3.3%:33.3%≈1/3,增长率从 33.3%到 3.3%缩小 10 倍,n要扩大 10倍,则3.3%=1/30。
(4)333%:增长率越大,n越小,333%=1/0.3。
【注意】增长率百化分之公式法(通用):1、如果遇到百分数实在想不起来,或者你就不想背,那么请记住“n=100/百分号前的数字(保留小数点后一位)”,是保底的方法,但不要因为这个方法就不学习前面的方法。
2、练习:42%,n=100/42=2.4,则42%=1/2.4。
二、比较类
【注意】增长量比较:1、识别:增长最多/最少、下降最多/最少。
(1)增长率比较:增长快/慢,形容速度。
(2)增长量比较:增长多/少,形容量。
2、两种题型:
(1)给现期量和基期量
①增长量=现期量-基期量
②若给柱状图,可直接比较柱状图的高度差(柱状图的高度差代表增长量)。
例:如图所示,给出 2016~2019 年的量,问哪一年的增长量最大?
答:直接看高度差,2017 年高度差最大。
(2)给现期量和增长率。
【注意】增长量比较:已知现期、r,求增长量。1、口诀:大大则大,一大一小百化分。
(1)大大则大:
①现期量大,同时r也大,则其增长量大。
②现期量大,同时|r|也大,则其减少量大。
(2)一大一小:百化分计算。
2、例:
(1)例 1:2018年,A有 200 块,同比增长 20%; B有 100 块,同比增长 10%。
答:A 的现期量大(200>100)、增长率也大(20%>10%),大大则大,则A的增长量更大。
(2)例 2:2018年,A有200 块,同比下降20%;B有 100 块,同比下降 10%。
答:比较减少量,看增长率的绝对值,A的现期量大(200>100)、|r|也大(|-20%|>|-10%|),大大则大,则A的减少量更大。
(3)例 3:2018年,A有 200 块,同比增长 20%;B有 100 块,同比增长 25%。
答:A的现期量大、增长率小,一大一小建议百化分(不建议野路子)。A:r=20%=1/5,则n=5,增长量=现期量/(n+1)=200/6=30;B:r=25%=1/4,则 n=4增长量=现期量/(n+1)=100/5=20,30+>20,则A的增长量更大。
第五节 比重
一、现期比重
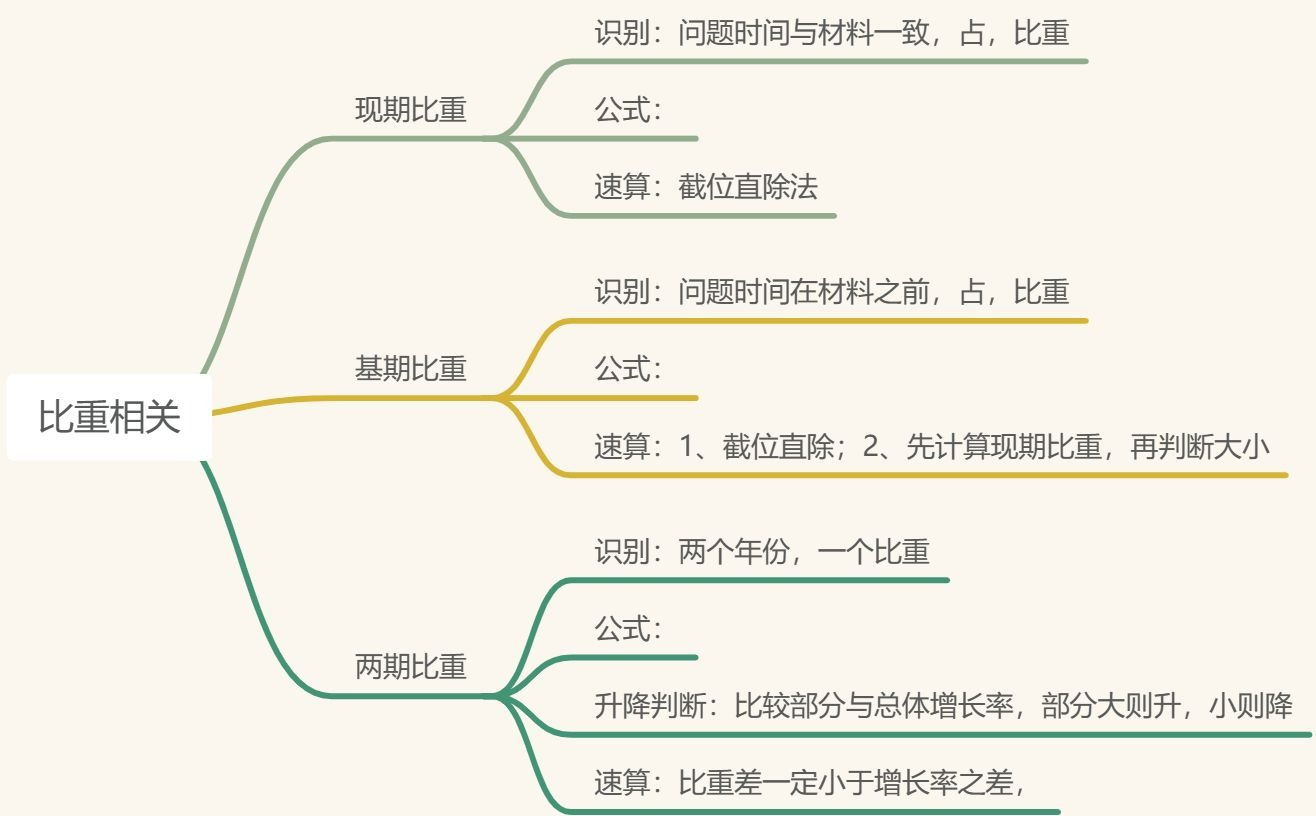
【注意】现期比重1、题型识别:问题时间和材料时间一致,······占······的比重
2、例:男生 30 人,全班 100 人,问:男生占全班的比重为多少?
答:男生是部分量,全班是总体量,比重=30/100=30%。
3、计算公式:
(1)
(2)”占“字前代表部分(A),”占“字后代表总体(B),,只需要根据文字找到“占”字前的主体和“占”字后的主体。
4、公式转化:
(1)给部分和比重,求总体:总体=部分/比重
(2)给总体和比重,求部分:部分=总体 * 比重
5、速算技巧:截位直除。
【注意】概念引申(比重的特殊表述形式)1、,也是比重,是两个增长量之间做除法。
例:2018 年我的家庭收入 20 万元,2017年10万元,其中我自己2018年收入2万元,2017年1万元,问:我对家庭总收入的增长贡献率?
答:“我”是部分,,即我对家庭总收入的增长贡献率为10%。
2、,代表利润在收入中的比重,联考中比较常见。
3、,事业单位考查不多。注意不要除反,应该先产 100件,卖了 90 件,所以产量是总体。
二、基期比重
【注意】基期比重:1、识别:问题时间在材料之前一基期,占、比重。
2、计算公式:。
3、例:问 2019 年我的收入占全家收入的比重?
推导:给 2020 年的数据,问 2019年,比重=“占”前/“占”后=2019年我的收入/2019 年全家收入,材料给的是 2020 年的数据,已知 2020 年,求 2019年,要分别用基期公式表示,我的收入现期量是 A,增长率是 a,全家收入现期量是 B,增长率是b,则所求=。
4、关键点:如何找部分与总体的量和增长率。A是部分(分子)的量,B 是总体(分母)的量,a代表部分的增长率;b代表总体的增长率,即大写字母代表量、小写字母代表率。
5、速算:
(1)公式为多步除法,选项差距大,分子分母都截两位,进行约分计算
(2)选项差距小:绝大多数情况符合:
①算一半:先算 A/B。
②看一半:再看(1+b)/(1+a)大于1或小于1,结合选项排除答案
(3)练习:=()。
A.45% C.50% B.47% D.57%
答:算一半:A/B=50/100=50%;看一半:(1+10%)/(1+5%)=1+,50% * 1+>50%,仅D项符合。A/B本质上是现期比重,有时候材料会直接给。
三、两期比重
【注意】两期比重:方法非常固定,公式推导可听可不听1、识别:两个时间+比重+升/降,两个时间求比重,为两期比重。问两个时间的比重谁高谁低,为两期比重比较
2、例:2013年1~9月,苏中工业用电量占江苏省工业用电总量的比重与去年相比
A.提高 B.降低 D.无法判断 C.不变
答:现“占”字,比重问题,两个时间(2013 年、去年),两期比重问题。选项是提高/降低,两期比重的比较问题
3、方法:瞪 a(分子增速)和b(分母增速)大小。
(1)a>b,今年比重上升
(2)a<b,今年比重下降
(3)a=b,今年比重不变
4、结论推导(不求甚解,只当涉猎):
(1)现期比重>基期比重→比重上升;现期比重<基期比重→比重下降。
(2)现期比重=A/B,基期比重=A/B * [(1+b)/(1+a)],A/B 都相同,判断现期比重和基期比重的大小,只要看(1+b)/(1+a)大于1还是小于1。当a>b,(1+b)/(1+a)>1,比重上升;当a<b,(1+b)/(1+a)<1,比重下降。
【注意】两期比重计算:1、识别:两个时间+比重+升/降多少百分点(具体百分点)。比两期比重比较多问了“百分点”
2、例:2015 年一季度,园区企业上缴税金占主营业务收入的比重比上年同期
A.上升了 0.1个百分点 B.上升了 3.1个百分点 C.下降了 0.1个百分点 D.下降了 3.1个百分点
答:占+两个时间(2015 年和上年),两期比重问题;不光问上升、下降还问具体的百分点,即两期比重计算问题。
3、公式:。推导:。此公式通常用不上,重点是记住结论。
4、结论:
(1)判升降:a>b,上升;a<b,下降。
(2)定大小:小于|a-b|。
5、结论推导(不求甚解,只当涉猎):。公式拆成三个部分:重点分析前两部分。
(1)A/B:代表现期比重,A/B<1。
(2)1/(1+a):一般情况下,a>0,1+a>1,则1/(1+a)<1。如果 a是负数,也不用纠结,做题中,负增长率很少,即使负最多负10%、20%,资料分析都是经济指标,不会负太多。
(3)A/B * [1/(1+a)]=1- * 1-=1-,则1- * (a-b)<|a-b| ,第一步已经判定完升降,第二步定大小时只需要看数值,因此对 a-b加上绝对值。
6、记住结论:50%的题目可以做出来。
(1)判升降:a>b,比重上升;a<b,比重下降
(2)定大小:两期比重差<|a-b|。
7、结论做不出来:代入两期比重差公式=(结合选项估算)
 比重公式总结
比重公式总结
| 现期 | 基期 | 升降判断 | 定量计算 | |
|---|---|---|---|---|
| 比重(占、比重) | a>b,比重上升; a<b,比重下降; a=b,比重不变。 |
两期比重差= 判升降,定大小 |
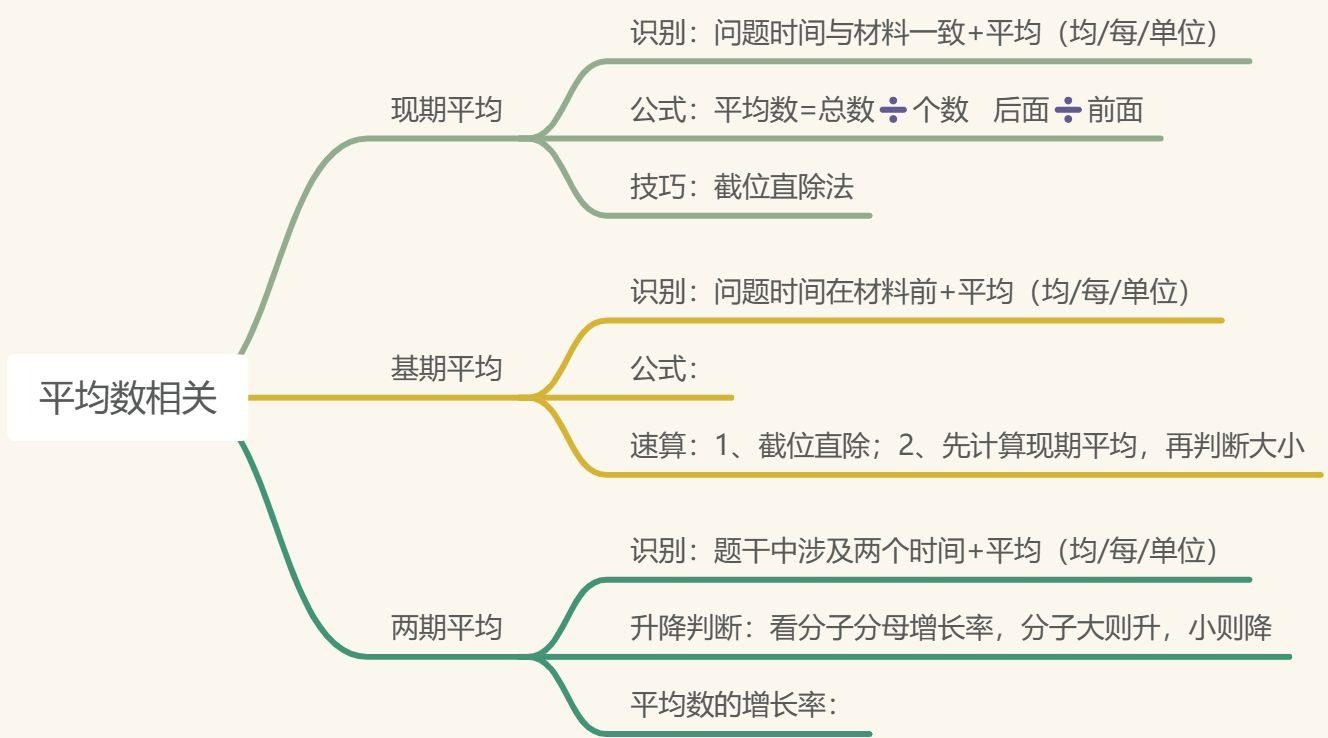
第六节 平均数
【注意】现期平均数:1、识别:问题时间与材料时间一致+平均(均/每/单位)。
2、公式:平均数=总数/个数=A/B。
3、计算形式(核心):后/前。
(1)人均收入=收入/人数,出现“均”箭头→平均数,“收入”在后,“人数”在前。
(2)单位面积产量=产量/面积,单位→平均数,“产量”在后,“面积”在前。
(3)平均每人次客运旅客运输距离=运输距离/人次,出现“平均”,“运输距离”在后,“人次”在前。
4、速算:截位直除。
【注意】基期平均数:核心“平均数=后/前”,与基期比重公式一样,区别在找数据方式不同,比重=“占”前/“占”后,平均数=后/前。
1、题型识别:问题时间在材料之前,平均数问法。
2、计算公式(与基期比重相同):A/B * [(1+b)/(1+a)]。A:分子的量;a:分子的增长率;B:分母的量;b:分母的增长率。
3、速算技巧:算一半、看一半。
(1)差距大:截位直除。
(2)差距小:先算 A/B,再看(1+b)/(1+a)与1的大小关系。
4、列式练习: 已知 2019 年公司有 100 人,同比增长 5%;总收入为 5000 万同比增长 10%。问 2018 年公司人均收入是多少?
答:问 2018 年,给 2019年,基期平均问题,人均收入=后/前=收入(对应A、a)/人数(对应B、b),A=5000万、a=10%、B=100 人、b=5%。
【注意】两期平均比较:和两期比重异曲同工。1、题型识别:两个时间+平均+上升/下降(高/低)。
2、记住结论:a为分子增长率,b为分母增长率。
(1)a>b,平均数上升。
(2)a<b,平均数下降。
(3)a=b,平均数不变。
3、易错点:a和b比较时需带正负号。
【注意】平均数的增长率(记住公式即可拿分):隶属于两期平均数计算的题型,属于特定题型。1、题型识别:平均/每/单位+增长了%。有平均数的题型和增长率的题型,两种题型放一起,就是平均数的增长率。
例:2018年某单位人均收入比上年增长了百分之多少?
答:人均收入→平均数,增长了百分之多少→增长率,本题为平均数增长率问题。
2、公式:,a是分子的增长率,b是分母的增长率,没有A、B,背下来即可。
3、推导:
4、做题逻辑:
(1)确定a和b。
(2)无脑代公式。
 比重、平均数公式总结
比重、平均数公式总结
| 现期 | 基期 | 升降判断 | 定量计算 | |
|---|---|---|---|---|
| 比重(占、比重) | a>b,比重上升; a<b,比重下降; a=b,比重不变。 |
两期比重差= 判升降,定大小 |
||
| 平均数(均、每、单位) | a>b,平均数上升; a<b,平均数下降; a=b,平均数不变。 |
平均数的增长率= |
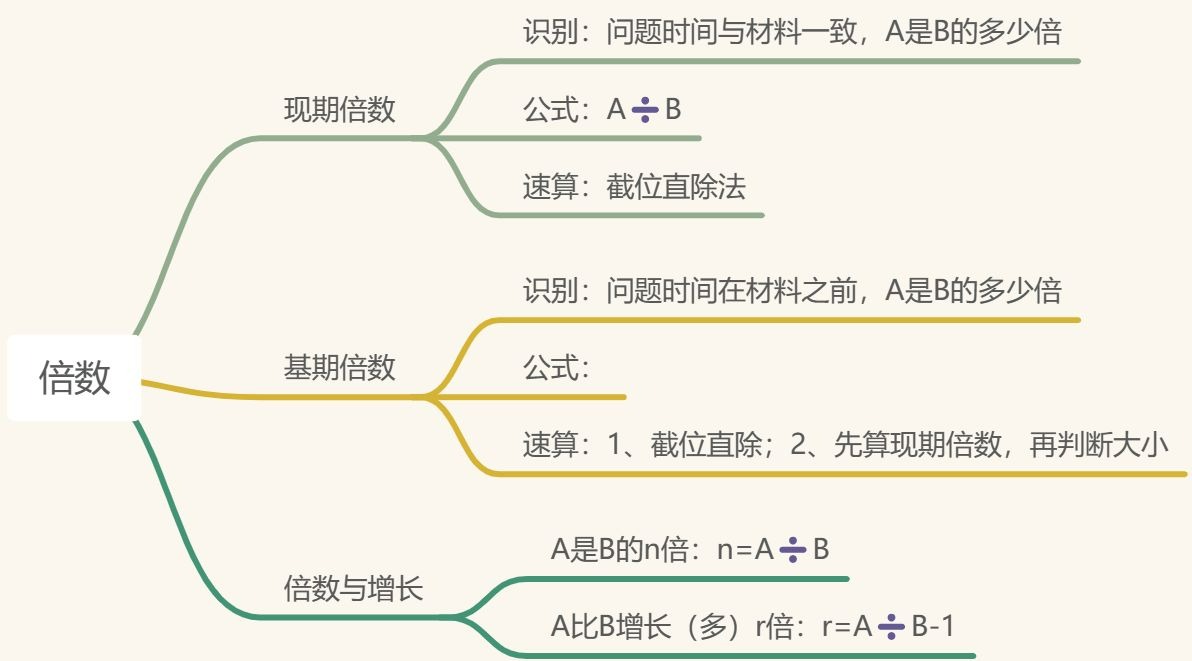
第七节 倍数
一、现期倍数
【注意】现期倍数:1、识别:问题时间与材料一致,A是B的多少倍
2、问法区分:
(1)A是B的几倍:A/B。
(2)A比B多/高/增长/增加几倍:多几倍=。坑点:问多几倍,一定要“-1”
二、基期倍数
【注意】基期倍数:和基期比重、基期平均异曲同工。1、题型识别:问题时间在材料之前,倍数问法。
2、计算公式:。A:分子,a:分子的增率,B:分母,b:分母的增率。
3、速算技巧
(1)差距大:截位直除(分子、分母都截)
(2)差距小:先算“A/B”,再看“(1+b)/(1+a)”与1的大小关系。
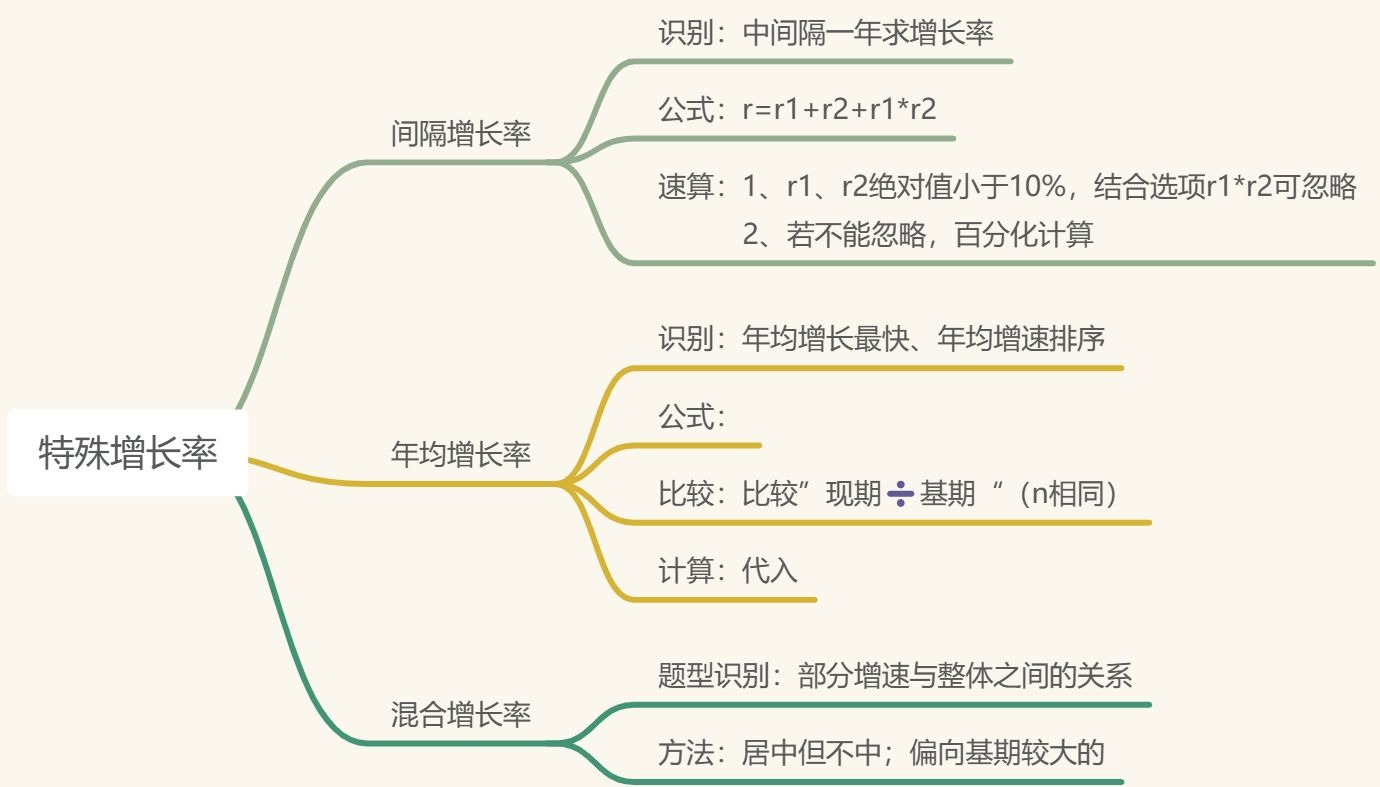
第八节 特殊增长率
一、间隔增长率
【注意】间隔增长率:1、识别:中间隔一年,求增长率。比如问 2023 年相较于 2021 年的增长率是多少,中间隔了一年(2022 年),求增长率,为间隔增长率问题。
2、公式:r=r1+r2+r1 * r2(先加和、再乘积)
3、公式怎么来:已知 2016 年与 2015 年同比增长率为 r1,2015 年与 2014年同比增长率为 r2,求 2016 年与 2014 年相比的增长率是多少?
答:假设 2014 年的量为 A,公式:现期=基期 * (1+r),则 2015 年=A * (1+r2),同理,再套一遍公式,2016 年=A * (1+r2) * (1+r1)。

4、r1和r2怎么找:r1、r2为现期和中间所隔年份的增长率。
(1)已知:2020 年比 2018年增长了百分之几?r=r1+r2+r1 * r2,r1是现期(2020年)的同比增长率;r2是中间所隔年份(2019 年)的同比增长率;即r1是今年的同比增长率,r2是去年的同比增长率。
(2)练习:
①2018 年比 2016 年增长了百分之几?r1是今年(2018年)的增长率,r2是去年(2017年)的增长率。
②2015 年比 2013 年增长了百分之几?r1是今年(2015 年)的增长率,r2是去年(2014 年)的增长率。
5、公式咋算:r=r1 + r2 + r1 * r2,加和比较容易计算,重点在于乘积。
(1)若 r1、r2的绝对值均小于 10%时,则 r1 * r2可以忽略。原因在于最大为10% * 10%=1%,若r1、r2的绝对值均小于 10%时,乘积<1%,往往可以忽略。
例:5%+8%+5% * 8%≈?
答:5%+8%=13%,5%、8%均小于10%,乘积可以忽略,原式=13%。
(2)否则,一个不变,另一个百化分,也可以直接乘。
例:18%+33.3%+18% * 33.3%≈?
答:18% * 33.3%=18% * (1/3)=6%,所求≈18%+33.3%+6%。
(3)计算核心:结合选项选答案。
(4)练习:关于乘积算不算,取决于选项。
①5.6%+6.3%+5.6% * 6.3%≈()
A.9.69% C.12.26% B.10.87% D.13.21%
答:先加和:5.6%+6.3%=11.9%,乘积先不用管,乘积>0,结果>11.9%,结合选项,排除A、B项;5.6%和 6.3%都小于 10%,则 5.6% * 6.3%<1%,所求=11.9%+1%<13%,对应C项。
②11.6%+20.4%+11.6% * 20.4%≈()
A.33.6% C.32.0% B.34.4% D.31.2%
答:先加和:11.6%+20.4%=32%,乘积>0,结果>32%,排除C、D项;11.6%、20.4均大于 10%,百化分计算,20.4%=1/5,11.6% * 20.4%=10 * % * (1/5)=2+%所求=32%+2+%=34+%,对应B项。
③8.5%+36%+8.5% * 36%≈()。
A.47.6% C.34.5% B.40.4% D.27.6%
答:先加和:8.5%+36%=44.5%,结果>44.5%,排除B、C、D项,对应A项
【注意】间隔增长率变型--间隔倍数:1、题型识别:间隔一年,求倍数。
2、例: 2023 年收入同比增长 20%,2022 年同比增长 10%,2023 年收入是 2021年的几倍?
答:已知 r1、r2,2023 年和 2021 年中间间隔一年,求间隔倍数。r=现期/基期-1=倍数-1,倍数=增长率+1,间隔倍数=r间隔+1,r 间隔=20%+10%+20% * 10%=30%+2%=32%,间隔倍数=32%+1。
3、计算方法:
(1)先求间隔增长率。
(2)间隔倍数=间隔增长率+1。
【注意】间隔增长率变型--间隔基期:常考1、题型识别:间隔一年,求基期。
2、例:2023 年收入为 A 亿元,同比增长 20%,2022 年同比增长 10%,2021年收入是多少亿元?
3、计算方法:
(1)先求间隔增长率。
(2)基期=现期/(1+r)→间隔基期=现期/(1+间隔r)。
二、年均增长率
【注意】年均增长率:1、题型识别:年均增长最快/最慢,年均增速排序。
2、计算公式:(1+r)^n=现期量/基期量,n 为现期和基期的年份差。年均增长量=(现期-基期)/n,年均增长量和年均增长率公式中的n含义相同。
推导:假设每年增长率均为r,2010年为A,2011年为A * (1+r),2012年为A * (1+r)²,2013年为A * (1+r)³,2014年为A * (1+r)^4=B,(1+r)^4=B/A,B/A 为现期/基期,“4”指的是年份差。
3、年均增长问题(年均增长量、年均增长率)基期的确定:若问“十二五“期间的总量,五年数据加和即可,不属于年均增长问题,基期不需要前推。
(1)具体时间段:2011~2015 年,基期为2011年,现期为2015年,年份差为 4。
(2)五年规划(全国规定):“十二五”期间(2011~2015 年),基期往前推一年,基期 2010 年,现期2015 年,年份差为5。
4、速算技巧:
(1)比较:n相同,比较现期/基期。比较类问题通常时间n相同,此时年均增长率取决于现期/基期,若现期/基期越大,年均增长率越大。
(2)计算:居中代入。近三年事业单位联考没有考查过,不需要担心。
三、混合增长率
【注意】混合增长率:特殊增长率中考查最多的,混合增长率问题无论是识别还是方法,理解含义即可。1、识别:求增长率;明显有部分混合得到整体的关系。
(1)例:已知进口额增长率、出口额增长率,求进出口额增长率。进口和出口混合得到进出口,已知两个部分的增长率,求总体的增长率,为混合增长率。已知男生增长率、女生增长率,求全班增长率,同样是混合增长率,有加和关系求增长率,就是混合增长率。
(2)常见加和方式:房产+地产=房地产,电信+邮政=邮电,1~2月+3 月=1-3月。
2、口诀:若男生平均身高 190 厘米、女生平均身高 180 厘米,全班平均身高不可能是 190+180=370 厘米,同理,混合增长率也不可能是两个增长率直接相加。
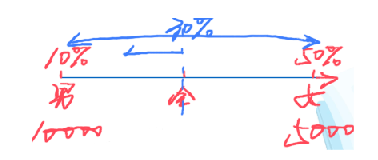
(1)混合后居中:最小r<总体r<最大r。如全班平均身高要介于男生平均身高和女生平均身高之间;一杯牛奶和一杯咖啡混合,味道介于两者之间。
(2)偏向量大的:哪个部分的基期量大,总体增速就向谁。
①如一大杯牛奶和一小杯咖啡混合,牛奶味道更重。
②“量”指的是基期量,做题时拿现期量近似代替基期量估算。
3、引例:2019 年某班男同学的花费总计为 10000 元,增速为 10%,女同学的总计为 5000 元,增速为50%。问:2019年全班花费的增速为多少?
A.8% C.38% B.23% D.52%
答:求全班花费的增长率,给的是男同学花费的增长率、女同学花费的增长率,男同学+女同学=全班,存在加和关系,求增长率,为混合增长率。混合后居中,男同学花费的增长率 10% < 全班花费的增长率 < 女同学花费的增长率 50%,结合选项,排除 A、D 项。偏向量大的,男同学花费 10000 元 > 女同学花费 5000元,全班花费的增长率偏向于男同学花费的增长率 10%,即全班花费的增长率位于中点的左侧,中点=(10%+50%)/2=30%,全班花费的增长率位于10%-30%,对应B项。
 比重、平均数、倍数公式总结
比重、平均数、倍数公式总结
| 现期 | 基期 | 升降判断 | 定量计算 | |
|---|---|---|---|---|
| 比重(占、比重) | a>b,比重上升; a<b,比重下降; a=b,比重不变。 |
两期比重差= 判升降,定大小 |
||
| 平均数(均、每、单位) | a>b,平均数上升; a<b,平均数下降; a=b,平均数不变。 |
平均数的增长率= | ||
| 倍数 | / | / |
注:a:分子增长率;b:分母增长率