图形推理

第一章 图形推理

【注意】图形推理：一般有5道题。

1、一组图：题干给出一组图，找到一个选项填入“？”处，让一组图连在一起形成规律。

2、两组图：第一组图用来找规律，找到规律之后应用到第二组图中选答案。

3、九宫格：规律形式比较多。

（1）横向观察（考得最多），第一行符合某种规律，第二行也符合该规律第三行应用该规律选答案；二是纵向（竖着）观察，第一列符合某种规律，第二列也复合该规律，第三列应用该规律选答案即可。这两种情况在考试中最常见基本上占了联考真题中 95%以上的九宫格题目，出现九宫格且没有思路时，优先横向观察（考得最多），其次纵向观察。

（2）特殊规律（简单了解即可）：“米”字型规律（每条线上的三幅图连一起都有规律）、“0”型规律（与最中间的图无关，外边的八幅图围成圈有规律）、”S“型规律（比如S型走位，九幅图连在一起有规律）以及对角线规律（对角线的5个图有规律）。

4、分组分类：将六幅图分为两组，要求每一组都有各自的规律，如一组为轴对称、一组为中心对称。

5、空间类：立体图形，下节课会讲解。

6、5 道图形题，一般考查4个平面题、1个立体题比较常见，也会出现3个平面题、2 个立体题。

【注意】图形推理学习的重点：

1、图形推理的考点：首先需掌握图形推理会考查什么规律，这样做题才能有思考方向，要了解位置规律、样式规律、属性规律、特殊规律、数量规律、空间规律。

2、很多同学可能课上听懂了，但课后自己做题还是做不出来，问题就在于没有识别图形特征。看到一个图用什么规律需根据图形特征判断，根据图的长相推断考查哪种规律的可能性最高。当掌握了特征图，看到图形特征，优先考虑可能性大的规律，再考虑其他的规律，要掌握思考的推理逻辑。

第一节 位置规律

【注意】位置规律：

1、识别特征：元素组成相同。考查位置变化，元素组成相同，但是位置不一样。如上图，每幅图均有4个黑球，其余均为白球，即为元素组成相同，唯一的区别在于黑球的位置不同，所以考查位置规律。

2、考法：

（1）平移（必考考点）。

（2）旋转、翻转（偶尔考查）。

考点一：平移

【注意】平移：

1、方向：朝哪个方向移动。

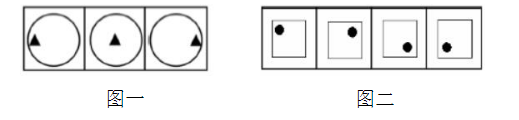
（1）直线走：上下、左右移动。如图一，图1中黑三角在最左侧，图1到图 2，黑三角向右移动到了中间；图2到图3，黑三角向右移动到了最右侧，即黑三角沿直线从左向右平移。

（2）绕圈走：顺、逆时针。如图二，每幅图中黑点依次位于左上角、右上角、右下角、左下角，黑点从左到右，将轨迹连接起来，即黑点依次沿顺时针方向平移。

2、步数：走几步。

（1）恒定（常见）：每次走的步数一样多，如每次都走 1步或每次都走 2步。

（2）递增：如依次移动 1、2、3、4步。

（3）无论是恒定还是递增本质上都是等差数列，也有可能会考查递减，但考查的概率极低，如依次移动4、3、2、1步，即越走越少，但很少见。主要还是考查递增和恒定不变，且图形推理中只要涉及数字规律，基本上都是恒定不变和递增。

【注意】宫格类：平移方向有很多种选择（左右、上下、顺时针、逆时针），技巧为看中间（内圈），判方向。

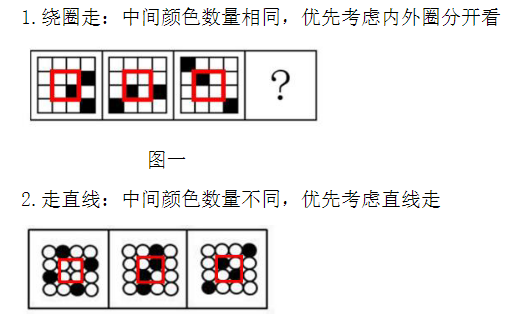
1、绕圈走：若中间颜色数量相同，则优先考虑内外圈分别移动。如图一，先圈出内圈（红色框），每幅图的内圈均只有1个黑块，中间内圈的颜色数量相同优先考虑内外圈分别进行平移，规律为内圈黑块沿内圈“田”字格依次顺时针移动 1格。图1外圈的黑块（第二行、第四列）按顺时针沿外移动1格，图1外圈的黑块（第四行、第四列）按顺时针沿外圈移动3格，即为内外圈分别平移内圈走内圈的，外圈走外圈的。

2、走直线：若中间颜色数量不同，则优先考虑按直线移动。如图二，先圈出内圈（红色框），每幅图内圈的黑球数量依次为 0、2、2，中间内圈的颜色数量不同，优先考虑沿直线移动，如左右走或者上下走。

【注意】走直线：先判定方向，再确定路径。

1、方向：

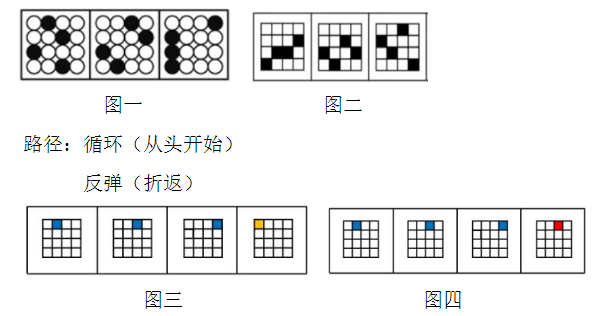
（1）每行数量（一般看黑球/黑块的数量）不变，按行左右平移。如图一每幅图的每一行均只有1个黑球，即每行数量不变，所以考虑按行左右平移，以第一行的黑球为例，图1到图 2，第一行的黑球向右移动了1格；图2到图 3，第一行的黑球继续向右移动了1格，这即为按行左右平移。

（2）每列数量不变，按列上下平移。如图二，三幅图的每一列均只有1个黑块，即每列数量不变，所以考虑按列上下平移，以第一列的黑块为例，图1到图 2，第一列的黑块向上移动了1格；图2到图3，第一列的黑块继续向上移动了1格，这即为按列上下移动。但看第二列黑块的移动会遇到一个问题，图1到图 2，第二列的黑块向下移动了1格，图2中第二列的黑块移动到头了，此时涉及到平移路径的选择。

2、路径：

（1）循环走：从头开始。如图三，图1到图 2，蓝块向右移动了1格；图 2到图 3，蓝块向右移动了1格，图3中蓝块走到头了（最右端），图4中回到起点（最左端）从头开始，即从起点走到终点无路可走了，则可以回到起点从头再来一遍，这即为循环。

（2）反弹：进行折返运动。如图四，图1到图2，蓝块向右移动了1格；图 2 到图 3，蓝块向右移动了1格，图3中蓝块走到头了（最右端），撞墙就回头，图4中蓝块退回到刚才的位置原路返回，如体能测试中的折返跑，从起点跑到终点，再从终点原路返回，这即为反弹。

（3）不用背路径，需根据已知图选择的路径判断，与己知图的路径保持一致即可。

考点二：旋转、翻转

1、旋转

【注意】旋转：钟表/手表指针做的运动就是旋转。

1、方向： 顺时针、逆时针。

2、常见角度：如图一，从左到右观察，规律为箭头依次顺时针旋转 45°一般考恒定的角度，加大难度可以考递增的规律，比如转动 90°、180°、270360°。像 45°、90°、180°，这些角度比较常见，因为用肉眼可以区分，没有什么争议，60°、120°、135°、150°考查比较少。

3、表盘类、钟表类特征图要记住，考查旋转。旋转的知识点掌握上述这些内容就够用了。

【注意】翻转：翻转类似于翻书，如将书翻到 60 页，再将书合上，与没翻之前没有任何区别，翻转之后的图会呈现轴对称的特征。

1、左右翻转：两个图沿竖轴呈现轴对称的特征。如图一，在2个三角中间画1 条线，将左侧的三角沿着中间的竖线翻转正好对应右侧的三角，2个三角沿着中间的竖线对折可以完全重合，呈现轴对称，即为左右翻转得到的。

2、上下翻转：两个图沿横轴呈现轴对称的特征。如图二，2个三角沿着中间的横线呈现轴对称，上下沿着横线对折之后可以完全重合，即为上下翻转得到的。

3、斜着翻转一般不出现，只考虑上下、左右即可。

【注意】如何区分旋转与翻转：

1、左右翻转：只有左右位置互换，上下位置不变。如图一，左右翻转只需换左右的位置，“黑眼睛”从左变到右，“白眼睛”从右变到左，“眼睛”一直在上“嘴巴”一直在正中间。

2、上下翻转：只有上下位置互换，左右位置不变。如图二，上下翻转只需换上下的位置，“黑眼睛”从左上变到左下，左右位置不变。

3、旋转 180°：上下、左右均互换。如图三，旋转 180°之后，“黑眼睛”从左上变到右下，“白眼睛”从右上变到左下，“嘴巴”从正下变到正上，即上下、左右都互换。

4、速记口诀：左右翻左右变，上下翻上下变，旋转 180°全都变。

5、考试中有可能旋转和翻转一起考，但是一个图既旋转又翻转，考查可能性比较低，一般是一个图形第一次旋转/翻转，然后翻转/旋转。

第二节 样式规律

【注意】样式规律：

1、识别特征：元素组成相似。位置规律的图形特征为元素组成相同，只有位置不同，但构成的元素都一样。但样式规律的图形特征为元素组成相似，即构成的元素不完全相同，只有局部相同。如上图所示，第一行，图1和图2左右两侧的斜线的长短和位置完全相同，图2和图3中间的斜线的长短和位置完全相同即为长得不完全相同，只有局部相同，称之为元素组成相似。

2、考点：可能会考査三个考点，即遍历、加减同异、黑白运算，其中最喜欢考查黑白运算，比较常见：遍历最近几年没有考过，以了解为主，加减同异在2019 年A类考查1道题，一般也不怎么考，所以重点是黑白运算。

考点一：遍历——缺啥补啥

【注意】遍历（缺啥补啥）：从字面上理解为普遍经历，即纵观全图，所有图都要看（将所有图放到一起），而不是单独看两幅图的差异找规律。缺啥补啥，“共产主义”你有我也要有。

1、缺啥补啥：如图一，第一组图有圆、三角形、五角星，第二组图有五角星三角形，与第一组图相比缺少一个圆，则“？”处应选为圆的选项。

2、图形特征：相同元素重复出现。只有满足此特征，才能知道缺什么，即有参照物才能缺啥补啥。

3、遍历类型：主要有两种，即元素种类（什么形状）、颜色。如图二，从形状上看，第一组图有圆、五角星、三角形；第二组图有五角星、三角形，还缺少一个圆：从颜色上看，第一组图有空白、斜线、灰色：第二组图有灰色、空白，还缺斜线的，则“？”处应补充斜线圆，对应圆2。

考点二：加减同异

【注意】加减同异：近五年只有 2019 联考A类考过1次，了解为主即可。

1、图形特征：相同线条重复出现，指同一个位置、同样长短。如图一，第一行，图1和图2左右两侧的斜线的长短和位置完全相同，图1和图3上下的两条平行线的长短和位置也完全相同，元素组成相似，这即为相同线条重复出现（相同长短的线条在相同位置上重复出现），出现此特征，优先考虑加减同异。

2、运算法则：

（1）相加、相减；

①相加：类似于数学中的加法，如图二，图1“O”+图 2“十”=图 3，即将图1和图2简单叠加/合并（位置以及其他的都不用动）即可得到图3。

②相减：如图二，与数学中的减法同理，图3-图2“十”=图1“O”

（2）求异、求同：

①求异：去掉相同线条，保留不同线条。如图三，图1和图2求异，图1中的“○”在图2中没有，不同的“○”在图3中应被保留；图2中的“◇”在该图1中没有，不同的“◇”在图3中应被保留，图1和图2中间均有“十”相同的“十”在图3中应被去掉，这即为求异，全部的运算过程其实就是去同求异（去掉相同线条，保留不同线条）。

②求同：保留相同线条，去掉不同线条。全部的运算过程为去异求同，去掉两幅图的不同线条、保密相同线条即可得到答案，如图四，图1和图2只有中间的“十”是相同的，图1的“○”和图2的“◇”是不同的线条在求同的过程中应被去掉，所以求同后的结果为“十。

（3）大多数题目，若两幅图经过运算越来越趋于复杂化，则一般是相加；如果越变越简单，一般是求同、求异。

考点三：”黑白“运算

【注意】黑白运算：样式规律中最常考黑白运算，近几年的真题中也频繁出现。

1、特征图：背景图相同，相同区域颜色不同。

（1）背景图相同：如上图，每幅图的背景图均为“田”字格，这即为背景图，类似于买房子，自己家和领居家的格局是一样的。

（2）相同区域颜色不同：如上图，前两幅图的右上角均为白色，图3的右上角为黑色，三幅图的右上角有白有黑，这即为相同区域颜色不同。

2、解题方法：相同位置运算，即图1和图2 原封不动地叠加（不用旋转、翻转）得到图 3，不同颜色之间存在颜色变化的规律。如上图，根据三幅图的右上角可知“白+白=黑”，根据三幅图的左上角可知“黑+黑=黑”；根据三幅图的左下角可知“黑+白=白”；根据三幅图的右下角可知“白+黑=黑”。根据已知图总结出运算法则，然后根据运算法则在“？”处所在行计算结果即可。

3、注意：

（1）运算法则不用背，需具体题目具体找，因为每道题的运算法则可能都会变，没有统一标准，根据已知图找到该题的运算法则即可。

（2）“黑+白”不一定等于“白+黑”，如上图，“黑+白”和“白+黑”的运算结果不同，一个等于白、一个等于黑，顺序不同结果也有可能不同，需具体题目具体验证，不能死记硬背。

第三节 属性规律

考点一：对称性

【注意】对称性（最重要）：基本上每年都考，常见的分为两类，即轴对称、中心对称，以前上学时学习过。

1、轴对称：

（1）含义：图形沿自身的一条线对折，两个部分可以完全重合，沿着对折的线称之为对称轴。一幅图可能会有多条对称轴，以五角星为例，沿着每个尖角对折之后均可以完全重合，共有5条对称轴，为轴对称图形。

（2）特征图：核心特征为“等腰”元素，因为对折之后两侧会完全重合（沿条线对折之后两侧长得一模一样），所以一定会存在“等腰”元素。

2、中心对称：

（1）含义：图形原地旋转 180°之后可以与原图完全重合。如图二，无论将谁旋转 180°之后均可以与原图重合，均为中心对称图形。若想不通则可以转卷子，正看、倒看长得一样即为中心对称，如图三，A项正看、倒看长得一模-样（旋转 180°之后可以与原图重合），为中心对称。

（2）有些图容易混淆，将五角星旋转 180°之后无法与原图完全重合，所以五角星不是中心对称，仅为轴对称。

（3）特征图：

①平行四边形、“N、Z、S”及其变形图（以平行四边形、“N、Z、S”为基底做改造）。

②“大风车”图形（如图二的图 5）。

③两个相同图形反着放，如图二的图 6，两个相同的箭头一颠一倒摆放。

3、轴对称+中心对称：特别规整。

（1）如图三，图1沿横竖两条线对折之后两侧均可以完全重合，为轴对称；图2沿两条斜线对折之后两侧均可以完全重合，为轴对称；图3沿横竖两条线对折之后两侧均可以完全重合，为轴对称，将这三幅图均旋转 180°之后均可以与原图完全重合，也均为中心对称，所以这三幅图均为轴+中心对称。

（2）特征：包含相互垂直的两条对称轴。不用管有几条对称轴（8条、10条均无所谓），只要其中有两条对称轴相互垂直即为轴+中心对称。

（3）特征图：特别规整、规则，出现“十”字、“H”。

4、对称性的特征图简单概括为规整，即图形看着舒服。

考点二：曲直性

【注意】曲直性：

1、单纯根据曲直性可以直接选出答案的题目很简单，考查的频率也比较低，一般会复合其他规律考查，利用曲直性可以排除 1-2个选项，然后再根据其他规律选答案。

2、曲直性很简单，线条只有两种，即曲线、直线，所以将图形分为三类，即全曲线、全直线、曲+直。

考点三：开闭性

【注意】开闭性：了解即可，在历年联考真题中几乎找不到，开闭性指图形是否形成了封闭空间。

1、全封闭：内部有封闭空间与外界不连通

2、全开放：没有独立的封闭空间与外界是连通的。

3、半封闭：介于全封闭和全开放中间，如图三，图1的字母“R”上面是全封闭的、下面是全开放的，为半封闭；图2的上面是全封闭的、下面是全开放的，为半封闭。

4、若题干同时出现全封闭、全开放、半封闭，且要求分为两组，则可以将全封闭和半封闭归为一组，因为全封闭和半封闭均有封闭空间，将全开放单独归为一组，因为全开放没有任何封闭空间。

5、特征：特征图不鲜明，但有一类图出现时考査开闭性的概率最高，即完整的图形留了小开口，如图二，图1本身好好的圆非得留个小开口，如图三，图2的下方本身可以完全封闭但偏偏没封闭，目的就是为了考查开闭性。

6、曲直性不好找特征图，因为世界上只有两种线，即曲线和直线，每幅图均一定有曲线或者直线。

第四节 特殊规律

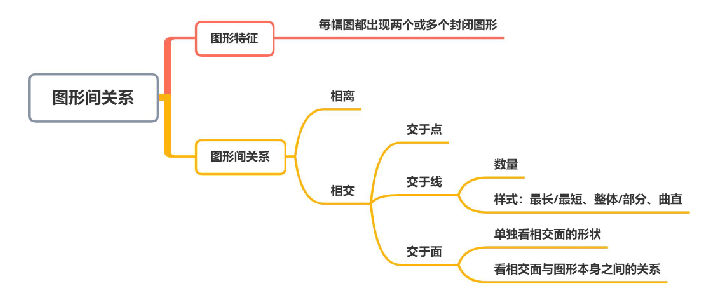
【注意】功能元素：这类题目并不难。

1、如何识别：特征图很容易识别，每幅图均有相同的小元素出现。如给出三幅己知图，每幅图均有1个小箭头，这个小箭头即为功能元素。每幅图均有多余且相同的小元素，如黑点、白点、箭头、8、x、√等，即为功能元素题目。

2、功能元素本身无任何含义，本质上就是标点符号，起标记作用，距离谁最近就标记谁，用标记什么选答案即可。

3、可以标记什么：以功能点为例，换成其他的功能元素（圆圈、箭头、三角形、x）均可，因为功能元素本身没有任何含义，只是标点符号而已。

（1）点：交点。如图一，蓝点与两条直线的交点完全重合，所以蓝点标记交点；红点标记曲线和直线相交所产生的交点。

（2）线：长短/曲直。如图二，红点和蓝点均距离线条最近，红点标记最短的直线，蓝点标记最长的直线，除此之外，还可以区分标记直线/曲线。

（3）角：直角/锐角/钝角、大小。如图三，红点距离左侧和下方的线条均很近，难以区分距离谁更近，证明将这两条线均标记了，两条线组成的是角，可以区分标记直角/锐角/钝角，如图三，红点标记直角，蓝点标记锐角，还可以区分标记最大角/最小角。

（4）面：大小、单独/相交。距离谁都不近，不好判断时就默认标记了整个空间。如图四，蓝点距离上方的曲线（椭圆）和下方的直线均不近，不好判断所以默认标记了整个空间，蓝点和红点均标记面，可以区分标记最大面/最小面如图四，蓝点标记最大面，红点标记最小面。还可以区分标记相交面/单独面如图五，蓝点标记单独面，红点标记椭圆和四边形相交形成的公共面。

4、特殊：若每幅图均存在2个功能元素，则一般会考虑连线，因为2个功能元素标记的东西可能不一样，如图六，一个功能点标记角，一个功能点标记面不好判断，所以往往会将2个功能元素连线，然后看连线经过了什么（如图六，2 个功能点的连线经过了原图的1个交点），或者看连线有没有与原图的线条垂直、平行。

5、答疑：试卷不是彩色的，因为成本比较高，且比较容易区分，所以试卷均是黑白的，最多还会画灰色。

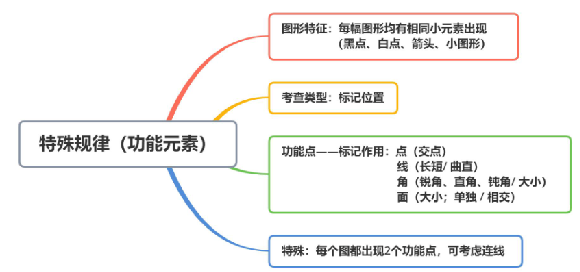
【注意】图形间关系：一般考查两个完整的几何图案之间有什么关联（位置关系）。

1、识别：每幅图均出现两个或者多个封闭图形时，可能会考查图形间关系因为最起码得能区分出有两个图形，只有一个图形无法看彼此之间的关系，有两个或者多个封闭图形才能看彼此之间的关系。

2、考点：相离、相交。

（1）相离（比较简单）：没有任何交集（谁也不挨着谁）。如图一，图1中的长方形和“笑脸”没有任何交集，且长方形将“笑脸”包含在内，细分为内含；图2中的三角形和“月亮”相离，但谁也没包含谁，细分为外离。内含和外离的本质均为相离。

（2）相交（形式较多）：比相离的情况多一些。

①相交于点：如图二，图1的椭圆与外部的矩形相切，依靠点产生交集，即为相交于点；图2也相交于点。

②相交于线：有一段线或者多段线是共用的。

a、相交线的数量：如图三，图1的黑矩形与外部的六边形共用上下两条线即相交于两条线；图2内部的黑图案与外部的三角形相交于三条线。

b、相交线的样式（长/短、整体/部分、曲/直等）：如图四，区分长/短，图1 相交于最长边，图2相交于最短边；区分整体/部分，图3相交于梯形的部分边、矩形的整条边，图4相交于两个图形的整条边，图5相交于两个图形的部分边；区分曲/直，图6相交于曲线，图7相交于直线。

③相交于面：两个图形产生公共的封闭空间。如图五，图1的两个三角形之间有交集，产生了公共的封闭空间，即相交于面；图2的两个“L”形产生了公共的封闭空间，即相交于面。

a、相交面的形状：如图五，图1的相交面为三角形，图2的相交面为五边形。

b、相交面与图形本身的形状是否一致：核心仍然为看相交面的形状。如图五，图3中两个大三角形相交之后形成的公共面仍为三角形，即公共面的形状与原图本身的形状相同（均为三角形）；图4中两个正方形相交之后形成的公共面仍为正方形，即公共面的形状与原图本身的形状相同（均为正方形）。

第五节 数量规律

知识点1：面

【注意】知识点 1：面。面比较好数，因为面比较宏观、比较好看。

1、什么是面：空白的封闭区问（窟窿）。

（1）面是空白的，黑色的不是面，所以面俗称“窟窿”。

（2）如果看到图形有“窟窿”，就可以数面。如图一，有6个封闭空问，即有6个面；图二有5个面，中间的黑色部分不是面。有几个独立的封闭空问就有几个面。

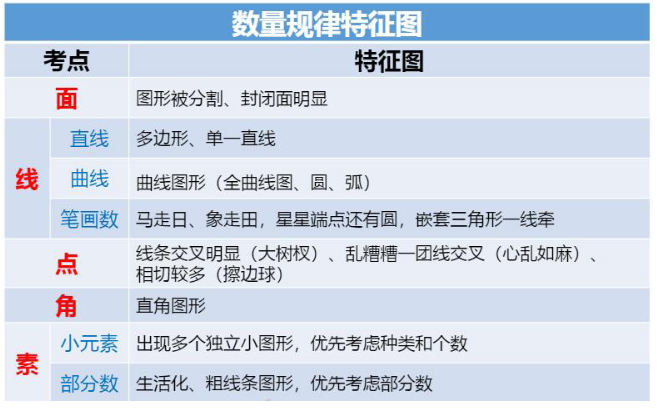
2、面的特征图：图形被分割、封闭面明显，考虑数面。数量规律会考虑面线、点、角、素，具体先数哪个就要根据特征图区分。

（1）图形被分割：如图三，类似于切蛋糕、切披萨，用“刀”将整个面进行切割，内部被切出多个小块，切出的块数越多，面就有越多。

（2）封闭面明显。如图四，封闭面明显，上面的2个“彩旗”、下面的 2个“底座”都是独立的封闭空问，分别是1个面。

（3）简单记忆就是“窟窿”，“窟窿”多就是面多，考虑面的数量。

【注意】面的细化考法：

1、什么时候想细化：出现数面特征图，但整体数面无规律或选不出唯一答案时，考虑面的细化考法，考查面的形状。

2、细化考法：

（1）所有面：如图一，图1有5个面，全部都是三角形；图2有5个面，全部都是四边形，可以考查所有面的形状是否相同，其中考查最多的是三角形面、四边形面。

（2）部分面（相同形状的面、某一形状的面）：所有面的形状不一致，则退而求其次，考虑部分面的形状是否可以一致。

①相同形状的面：看一幅图中有几个面的形状是一致的。如图二，图1有5个三角形面的形状是一致的，即有5个相同形状的面；图2有4个面，其中有3个相同形状的面，外面的3个梯形完全一致。

②某一形状的面：将所有面都放在一起，只数一种形状面的数量。如图二，图1有6个面，其中有5个三角形形状的面，图2有1个三角形形状的面。数面的时候独立来数，不能合并，所以不能认为图2外面还有3个三角形面。再如图3，只有1个三角形面，外面的大三角形在事业单位考试中一般不计算在内，计算在内的题目非常少，一般不需要合并，在公务员考试中可能会计算在内。

3、图形部分每年考査5道题，每种规律考查几道题无法确定。

【注意】单个面（最大、最小）：部分面也没有规律，考虑单独的、特殊的面，看特殊面的形状，一般看最大面、最小面。

1、如图一，图1的最大面是三角形，图2的最大面是平行四边形，则看最大面的形状（如三边形、四边形、五边形），最小面同理。

2、看最大面、最小面取决于图形。如果每幅图明显存在最大面，毫无争议，考虑最大面；同理，如果每幅图明显存在最小面，毫无争议，考虑最小面。

知识点2：线

【注意】知识点 2：线。所有的图都是由直线和曲线构成，所以数直线和曲线的条数。

1、直线特征图：多数图形都是由多边形组成，或者出现单一直线，考虑数直线数。

（1）一般几边形就有几条直线，如三边形、四边形、五边形，就是根据边的数量命名的。

（2）出现单一直线，没有形成图形，目的就是凑数。

2、曲线特征图：曲线图形比较多，如全曲线图、圆、弧比较多，考虑数曲线。

3、所有图不是直线就是曲线，所以出现特征比较鲜明的图，优先数线的条数。

4、曲直分开数，不要将所有线条混在一起数，可能找不到规律，有可能单独考查直线数、曲线数，或者直线数和曲线数求和、求差。

5、如何区分线的数量：

（1）直线：直着的、完整的1条线，就是一条直线。如图二，图1有2条直线，是完整的2条直线；虽然中间有交点，公务员考试会从中间断开，算3条直线，但是在事业单位考试中正常情况都不拆开；再如“x”，一般算2条直线。

（2）曲线：平滑过渡的就是1条曲线。如图四，图1圆上虽然有多条直线与之相较，但是数曲线的时候就算1条曲线，即任何1个圆或者椭圆都是1条曲线。再如”奥迪”车标，4个圆依次相交，有4个圆，就是4条曲线。如图四，图2本来平滑过渡，中间的走向突然发生变化，出现拐点，则是2条曲线；可以想象用铁丝做成这种形状，摸到中间的拐点，会感觉“扎手”，则不是1条曲线而是2条曲线。如图五，平滑过渡，摸任何地方都不“扎手”，则是1条曲线。

【注意】线的细化考法：

1、什么时候想细化：出现数线的特征图，但整体数线无规律或选不出唯一答案，考虑线的细化。

2、怎么细化：一般针对直线细化，曲线没有细化。

（1）按方向分：横线和竖线分开数。出现“十”字、横平竖直的图案，即横线和竖线比较多，考虑横竖分开数。如图一，整体数线无规律，分开数线，每幅图均有3条竖直方向的线。

（2）按位置分：内外分开数。题干出现比较多的多边形、单一直线，且有明显的外框，内外分明，考虑内外分开数。如图二，每幅图都有明显的外框，内部有小图案，内外分明，考虑内外分开数。只有图4有1条曲线，其他图均没有曲线，所以数直线。外部直线数依次为6、5、4、4、5，内部直线数依次为 5、4、3、3、4，外部直线数-内部直线数=1，据此找答案。

（3）内外分开数考查较多，联考很少考查横竖分开数，所以优先考虑内外分开数。

【注意】笔画数：常规数直线、曲线条数比较简单，难点在于笔画数问题，而笔画数问题每年必考，所以要认真听讲，不要走神。

1、一笔画：图形一笔即可画成，线条不能停、不能间断，也不能重新起头。如图一，比较简单，均一笔就可以画出来，所以均为一笔画图形。但有些图会比较复杂，如图二，如果尝试用笔画出来就会掉入出题人的陷阱。做笔画数的题目不要尝试画出来，可能会浪费时问，也可能找不到最简便的画法（可能用三笔画出来，而简便画法只需要一笔即可）。图二确实可以一笔画成，按照右侧的箭头方向即可画出来，但是比较复杂。

2、后面所有的题目都不会告诉大家应该如何画出来，也不要问如何画出来只需要能计算出来即可。

【注意】一笔画：

1、一笔画的判定方法：同时满足以下两个条件，缺一不可。

（1）线条之问全部连通。图形想要一笔画出来，就要保证图形的线条全部连在一起。如图一，无法一笔画成，因为内部的线条与外框没有挨在一起，肯定无法一笔画成，一笔不能画出完全不相连的两条线。再如图二，一笔无法画出来，没有任何交集。

（2）奇点数为0个或2个。

2、奇点：发射出奇数条线的点。奇数指无法被2整除的数，如 1、3、5、7、9、11、10001。

（1）判断一个点是否是奇点，就看发射出几条线。如果发射出奇数条线，则该点为奇点。

（2）如图三，红点发射出1条线，1是奇数，则该点是奇点。

（3）如图四，图1的蓝点发射出2条线，2不是奇数，则该点不是奇点；图2的黄点发射出3条线，3是奇数，则该是奇点；图4黄点发射出5条线，5是奇数，则该点是奇点；如果一个点发射出201条线，201是奇数，则该点也是奇点；图3的黄点发射出3条线，3是奇数，则该点是奇点。

（4）如图四，想要判断图3的黄点发射出几条线，可以想象成站在该点上，有3条路可走，则发射出3条线，3是奇数，该点是奇点。如图五，假设从下方红点出发，想象成站在红点上，有3条路可走，则发射出3条线，3是奇数，该点是奇点；同理，上方的红点也是奇点。

（5）数发射出几条线的时候，与直线、曲线无关。如图六，考虑从红点出发，有4条路可走，则发射出4条线，4不是奇数，该点不是奇数；同理，上面的交点也不是奇点。

（6）考试的时候不会给出红点，不会将交点标记出来，需要自己寻找。

3、数奇点的时候不要忘记数上端点，所有的端点都是奇点，因为端点只发射出1条线。如一条线段，线段的两头就是端点。但前提是独立的、不与任何线条挨着，否则应该是交点，如图七右侧的点是交点。

（1）如图八，1号端点只向右发射出1条线，1是奇数，则该点是奇点：2号端点只向左发射出1条线，1是奇数，则该点是奇点。

（2）如图九，图1的2个红点是端点，均发射出1条线，1是奇数，均是奇点；下方的蓝点发射出2条线，2不是奇数，所以下方的蓝点不是奇点，共有2个奇点。图2的3个端点均发射出1条线，1是奇数，均是奇点；下方的黄点发射出3条线，3是奇数，则是奇点，共有4个奇点。图3的3个端点均发射出1条线，1是奇数，均是奇点；上方的黄点发射出3条线，3是奇数，则是奇点共有4个奇点。

（3）如图十，图1右侧的2个交点均发射出3条线，3是奇数，均是奇点；左侧的2个交点均发射出2条线，2不是奇数，均不是奇点，共有2个奇点，且是连通图，一定是一笔画图形。图2左侧的交点发射出4条线，4不是奇数，所以不是奇点；中间的交点发射出4条线，4不是奇数，所以不是奇点，共有0个奇点，且是连通图形，则是一笔画图形。一堆圆相切，不管有多少个，均是一笔画图形，切点均不是奇点。图3边上的4个交点均发射出3条线，3是奇数，均是奇点；中间的交点发射出4条线，4不是奇数，不是奇点，共有4个奇点，不是一笔画图形，涉及多笔画问题。

【注意】多笔画：

1、图形笔画数=奇点数/2。奇点数多于2个，则用奇点数除以 2，等于几就是几笔画。

（1）奇点数一定是偶数个。如果数出来的奇点数是 3、5、7、9······个，说明一定数错了，要重新来数。所有图形都是由线段组成，一条线段白带2个端点，2个端点都是奇点，无论如何组合，奇点数一定是2的倍数。

（2）如图1的左侧中间的交点和中间的交点都是奇点，2个端点也是奇点，共有4个奇点，4/2=2，是两笔画图形。

2、多部分图形的笔画数：将每个部分的笔画数分别数出来，再相加。如图 2，由2个图形组成，线条不相连，则将每个部分的笔画数分别数出来，再相加才是总笔画数。内部“十”字有4个奇点，中间的点发射出4条线，不是奇点，4/2=2内部是两笔画；外部的圆是一笔画，加起来是三笔画图形。

【注意】笔画数特征图：“马走日、象走田，星星端点还有圆”“嵌套三角形一线牵，杂乱的面数奇点”。特征图会随着考试的变化逐渐更新。加粗的字代表特征图，其他的字只是为了押韵，没有用。

1、“日”指“日”字及其变形图，一般都是一笔画图形。

2、“田”指“田”字及其变形图，一般都是两笔画图形。红框框出来的图形也是“田”字的变形图，只不过将“十”字挪到了框外面。

3、出现类似于星星的图案，一般都是一笔画图形。

4、“端点”指多端点图形，端点比较多，可以考查很多种笔画。

5、“圆”指圆相切、圆相交，一般都是一笔画图形。

6、“嵌套”如最后一行图 3、4，是嵌套图形，不同的封闭图形叠加在一起，可以考査笔画数。如图 3，上面的“L”形与下面的封闭图形叠加在一起：如图 4，左右2个曲线图形与圆叠加在一起。

7、图形中三角形面比较多，除了可以考査三角形面的数量，也可能考查笔画数。

8、“一线牵”图形如右下角的图形，一条线牵着两个封闭图形。

9、有些题目有数面的特征，如最后一行后四幅图，可以考查数面；但是数面没有规律，立刻要考虑笔画数，这是根据真题中的考查频率确定的。

10、以上都是笔画数的特征图，具体是几笔画不要背，最好是数奇点。

11、出现笔画数的特征图，考虑数笔画。

知识点3：点

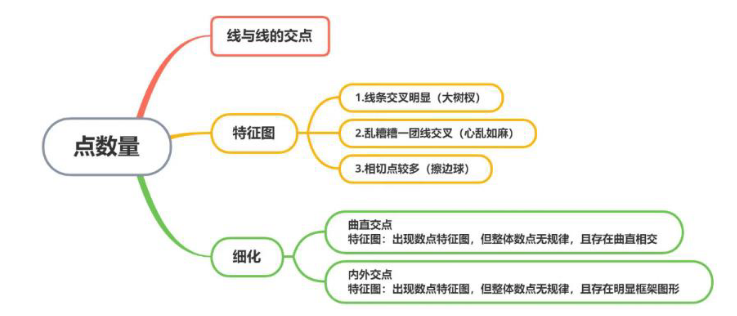
【注意】点数量：

1、什么是点：线与线的交点，即看有几个交点。

（1）如图一，图1中2条直线产生1个交点，图2中2条曲线产生1个交点。

（2）如图二，图1中的点虽然学名叫顶点，但也是2条直线相交产生的点，也算交点；图2虽然是切点，但也是圆和直线相交产生的点，也算交点。

（3）只要两条线产生公共点，相交在一个点上，就算交点。注意切点、顶点都是交点，但是端点不是交点。

2、数点的特征图：有3类特征图，老师分别起了3个比较通俗的名称，即“大树杈、心乱如麻、擦边球”。

（1）大树权：指的是线条交叉明显，就像外边没有修剪的树权一样，比较杂乱，容易考查交点，如图三。

（2）心乱如麻：乱糟糟一团线交叉，越乱交点越多，如图四。

（3）擦边球：相切较多，就像打桌球一样，贴着案子边打，切点越多，交点越多，如图五。

【注意】点的细化考法：

1、如果出现数点特征图，但整体数点无规律，则考虑点的细化（有2个方向的细化）。

2、点的细化考法 1： 如果题目中存在曲直相交，可以单独考虑数曲直交点（不数点的总数，单纯看曲线和直线的交点）。如上图，有3个曲直交点。

【注意】点的细化考法2：内外交点。如果题干存在明显的框架图形，如每幅图中均有一个圆形（正方形）的封闭图案作为框架，与原来的图案相交，可以考虑框上、框外、框内交点，也就是内外交点，以框区分出内外，分别数交点。如上图，以圆作为框架图案，框上交点指的是在圆上相交的交点，框外交点指的是圆边框以外的交点，框内交点指的是圆内部的交点。

知识点4：角

【注意】角数量：近五年的联考真题没有考查过角数量，了解为主，大概率不会考查。

1、什么是角：直线与直线相交形成的图案叫做角，曲线不行，必须是直线与直线相交。

2、数角一般数小于 180°的角。如图 1，如果数角，只有1个直角。

3、由于角本身就不喜欢考查，所以考试时不会优先考虑数角，实在没招、想放弃的时候可以考虑数角。如果题目中有特殊的直角，可以优先考虑数直角。

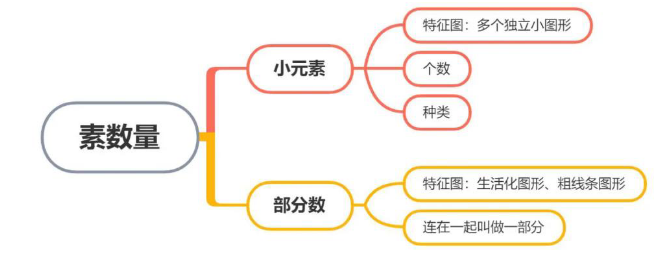
知识点5：素

【注意】素数量：“素”指组成图形的元素，如图形由圆圈、黑点、”X、√、S、王”等组成，组成图形的任何一个小部分均可以称为元素。

1、元素个数：如图一，图1有2个雪花：图2有2个圆环+1 条斜杠，有 3个小元素；图3有4个小元素：图4有5个小元素。再如一个“○”上打个“√”有2个小元素，一个“√”，一个“O”。

2、元素种类：

（1）看的是形状：如图二，图1中4个“+”长得一模一样，算一种元素，但是有4个元素；图2两个黑色三角形长得一样，算一种元素，六边形是一种元素，所以有两种元素；图3圆、六边形、三角形是三种元素。

（2）如果出现一个大白圆、小白圆，通常可以算一种元素，因为都是圆但是如果是一个白圆和一个黑圆，一般算两种元素，因为颜色不一样。

3、答疑：图一可以数元素种类，依次为 1、2、3、4 种元素。

4、特征图：一般考査元素的题，都是出现多个独立的小图形。如图三，每幅图中均出现了多个独立的小图案，一般喜欢考查元素。

【注意】部分数：

1、部分数：连在一起就叫做一部分。

2、如上图，图1“叶子”图案虽然复杂，但是线条全部连在了一起，所以是一部分；图 2“飞机”的“翅膀”和“机身”中问有缝隙，没有连上，是两部分；图3“辽”中“、”“了”和“辶”均是独立的，是三部分；图4有1个圆圈4 个“脚趾”、1个“脚掌”，加起来是六部分。

3、特征图：出现生活化图形（图案与生活中的物品可以联系在一起，如图 1是“叶子”，图2是“飞机”，图4是动物的“脚掌”，均为生活化图形）、粗线条图形（上述4幅图均算粗线条图形），喜欢考查部分数。

第六节 空间重构

1、折叠方向

【注意】

1、折叠方向：题干给出的均是纸盒的外表面展开图，意味着图1的折叠方式是正确的，折成立体图形之后，面上面带的图案需要露出来，如果将图案折在内部，则什么都看不到，因此图2的折叠方式永远都是错的。

2、所有的方法都是排除法，排除3个错误选项，剩下的就是正确答案，不需要纠结正确的选项是怎样折叠出来的，具体怎样折叠需要靠空问想象能力。

方法一：相对面

【注意】相对面：老师讲解的例题均是正六面体，因为考试中考查最多，以后遇到不规则的六面体，老师讲解的技巧依然可以使用。

1、相对面：即2个面没有任何交集。比如大家现在在卧室或者教室，棚顶和地板、左边的墙和右边的墙、前面的墙和后面的墙均没有任何交集，均属于相对面。

2、如上图中，面A和面 F、面D和面 B、面E和面C为三组相对面。但是考试中一般不会给出透视图，给出的均是如图2所示的立体图，从立体图的顶点观察，能看到其中的3个面（面A、面D、面E），另外3个面被挡住了，看不见，此时会发现一个特点，面A和面F是一组相对面，在图2立体图中只出现了面 A，面F没出现；面D和面B这一组相对面在图2立体图中只出现了面D，面B没有出现；面E和面C这一组相对面在图2立体图中只出现了面E，面C没有出现，每一组相对面在立体图中均只出现了1个，这不是巧合、不是老师故意画的，而是特性，要求必然如此。

3、应用：在立体图中，一组相对面仅出现其中一个。如上图，面A和面F这一组相对面只能在图2立体图中出现1个，如果面A和面F同时出现，则选项定是错的；如果面A和面F同时未出现，选项也是错的，只有出现1个，才可能是正确的。

4、答疑：A、B、C、D、E、F 白己随便标记，考试时面上不会标符号，一般画的是图案，老师标字母的唯一原因就是为了方便讲解，考场做题时不用标记字母。

【注意】在展开图如何判断相对面：

1、同行或同列相隔一个面：如图一，图2中2个红色面同行问隔1个白色面，2 个白色面同列问隔1个蓝色面、2 个蓝色面同列问隔1个白色面，均为相对面。按照相对面的特点，图1的立体图不正确，因为2个红色面在展开图中是一组相对面，不可能在立体图中同时出现，因此立体图错误，排除即可。

2、“Z”字形两端（紧邻中线）：如果2个面处在“Z”字形两端，则是相对面。

（1）如图二，2个蓝色面不在同一直线上，用直线将2个蓝色面连接起来类似英文字母“Z”，所以2个蓝色面处在“Z”字形两端，“中线”指的是夹在“Z”字2条平行线中问的那条线，2个蓝色的面均紧挨着中线，中问不能被其他面隔开，均为一组相对面。

（2）如图三，从面a开始画字母“Z”，一直可以画到面 e，不能说面a和面e是一组相对面，因为面e没有紧邻中线，中问隔了面d，所以面a和面e不是一组相对面。面a和面d是紧邻“Z”字中线的一组相对面：面c和面e是同行问隔1个面的一组相对面；面b和面f是同列问隔1个面的一组相对面。

方法二：相邻面

【注意】平面图中构成直角的两条边是同一条边：

1、如图一，图1中面5和面2的2条绿色边构成直角，构成直角的两条边是同一条边，如图 2、图 3、图 4，折叠时2个面之问的角度不断缩小，最后会重合，所以2条绿色边是同一条边；同理，面5的左边和面4的上边构成直角、面3 的左边和面4的下边构成直角、面2的下边和面3的右边构成直角，均为同条边。

2、如图二，2 条红色边、2条蓝色边、2条绿色边均构成直角，均为同一条边。

3、答疑：

（1）面6和面4存在公共边，但是大家目前找不到，如果要找，也可以找到，面5的左边和面4的上边构成直角，是同一条边，因此面6的左边和面4的左边是同一条边。

（2）做题时并不是把所有的公共边全部找出来，根据选项做题。

【注意】相邻面方法 1：看相对位置

1、公共边有个特性，即折叠前后相邻关系保持不变，这就是利用相邻面的第个解题方法，即看相对位置。

2、如图一、图二，以箭头面为例，箭头面属于图形指向比较明显的面，可以看出箭头的“尖”和箭头的“尾巴”，明显可以分出上下，展开图中箭头的“尖指向的是“心形”面，折叠前后相邻关系保持不变就意味着选项中的立方体不管以什么角度折叠，箭头的“尖”永远都要指向“心形”面，如果箭头的“尖”没有指向“心形”面，选项必然错误，这就是固有特性。A项中箭头的“尖”指向的是“66”面，没有指向“心形”面，因此A项一定错误；展开图中箭头的“尾巴”对着“66”面，而B项中箭头的“尾巴”对着“月亮”面，因此B项也一定错。

【注意】相邻面方法 2——画边法：如果根据相对面、相邻面的相对位置均无法选出唯一答案，此时可以考虑画边法。画边法有三个步骤，老师会逐步讲解。

【注意】画边法：

1、第一步：结合选项，找一个特殊面的唯一点。

（1）特殊面：在已知图中，只有一个长得这样的面。如已知图中只有1个“x”面，就属于特殊面，万一有2个“ㄨ”面，则不属于特殊面。

（2）唯一点：在特殊面的4个顶点中找，看4个顶点中是否存在独一无!的点，不要在边上找，也不要在面的内部找，因为容易出错。

①面 a：每个顶点均往面的内部发射1条对角线，4个顶点完全一样，没有任何区别，因此没有唯一点。有同学认为立体图中面a右下角的点与面c的对角线相邻，因此认为面a右下角的点为唯一点，注意找唯一点时就在特殊面中找不要将其他的面作为参考。

②）面 b：2个绿点长得一模一样，没有区别，不是唯一点；2 个蓝点均引出 1条对角线，没有任何区别，没有唯一点。

③面c：绿点、红点均是唯一点，4个顶点中只有红点引出了半条对角线因此红点是独一无二的唯一点；4个顶点中只有绿点没有往面的内部引出对角线因此绿点也是唯一点；2个蓝点均引出同一条对角线，没有任何区别，不是唯一点。

2、找唯一点是在特殊面中找的唯一点，以图二为例，图1是已知图形，图 2是选项，不能在空白面中找唯一点，因为展开图中有2个空白面，不是特殊的面；面f也不存在唯一点，在面c中找唯一点最好找，面c中黑色矩形所在的点可以作为唯一点。找到唯一点之后，以唯一点为起点，在展开图和选项的面c中顺时针画边标号边 1-4（逆时针也可以，但是一定要保证同一方向）。

3、题干与选项对应面不一一排除。如图二，展开图中边1挨着面b，立体图中边1挨着面 f，对应面不一致，排除：也可以看边2，展开图中边2挨着面e，而立体图中边2挨着空白面，对应面不一致，排除。